|
8 | 8 |
|
9 | 9 | 如图所示,这 `3` 棵树都是二叉搜索树。 |
10 | 10 |
|
11 | | -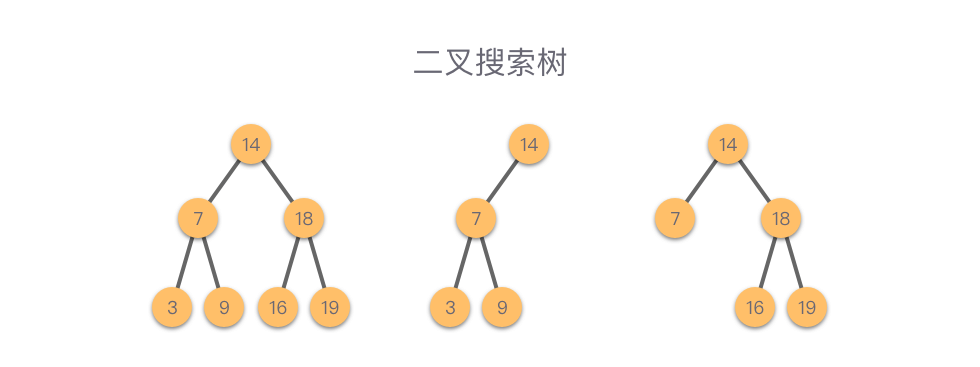 |
| 11 | + |
| 12 | + |
| 13 | +二叉树具有一个特性,即:**左子树的节点值 < 根节点值 < 右子树的节点值**。 |
| 14 | + |
| 15 | +根据这个特性,如果我们以中序遍历的方式遍历整个二叉搜索树时,会得到一个递增序列。例如,一棵二叉搜索树的中序遍历序列如下图所示。 |
| 16 | + |
| 17 | +## 2. 二叉搜索树的查找 |
| 18 | + |
| 19 | +> **二叉搜索树的查找**:在二叉搜索树中查找值为 `val` 的节点。 |
| 20 | +
|
| 21 | +### 2.1 二叉搜索树的查找算法步骤 |
| 22 | + |
| 23 | +按照二叉搜索树的定义,在进行元素查找时,我们只需要根据情况判断需要往左还是往右走。这样,每次根据情况判断都会缩小查找范围,从而提高查找效率。二叉树的查找步骤如下: |
| 24 | + |
| 25 | +1. 如果二叉搜索树为空,则查找失败,结束查找,并返回空指针节点 `None`。 |
| 26 | +2. 如果二叉搜索树不为空,则将要查找的值 `val` 与二叉搜索树根节点的值 `root.val` 进行比较: |
| 27 | + 1. 如果 `val == root.val`,则查找成功,结束查找,返回被查找到的节点。 |
| 28 | + 2. 如果 `val < root.val`,则递归查找左子树。 |
| 29 | + 3. 如果 `val > root.val`,则递归查找右子树。 |
| 30 | + |
| 31 | +### 2.2 二叉搜索树的查找代码实现 |
| 32 | + |
| 33 | +```Python |
| 34 | +class Solution: |
| 35 | + def searchBST(self, root: TreeNode, val: int) -> TreeNode: |
| 36 | + if not root: |
| 37 | + return None |
| 38 | + |
| 39 | + if val == root.val: |
| 40 | + return root |
| 41 | + elif val < root.val: |
| 42 | + return self.searchBST(root.left, val) |
| 43 | + else: |
| 44 | + return self.searchBST(root.right, val) |
| 45 | +``` |
| 46 | + |
| 47 | +### 2.3 二叉搜索树的查找算法分析 |
| 48 | + |
| 49 | +- 二叉搜索树的查找时间复杂度和树的形态有关。 |
| 50 | +- 在最好情况下,二叉搜索树的形态与二分查找的判定树相似。每次查找都可以所辖一半搜索范围。查找路径最多从根节点到叶子节点,比较次数最多为树的高度 $log n$。在最好情况下查找的时间复杂度为 $O(log_2 n)$。 |
| 51 | +- 在最坏情况下,二叉搜索树的形态为单支树,即只有左子树或者只有右子树。每次查找的搜索范围都缩小为 $n - 1$,退化为顺序查找,在最坏情况下时间复杂度为 $O(n)$。 |
| 52 | +- 在平均情况下,二叉搜索树的平均查找长度为 $ASL = [(n+1)/n] * log_2(n+1) - 1$。所以二分搜索树的查找平均时间复杂度为 $O(log_2 n)$。 |
| 53 | + |
| 54 | +## 3. 二叉搜索树的插入 |
| 55 | + |
| 56 | +> **二叉搜索树的插入**:在二叉搜索树中插入一个值为 `val` 的节点(假设当前二叉搜索树中不存在值为 `val` 的节点)。 |
| 57 | +
|
| 58 | +### 3.1 二叉搜索树的插入算法步骤 |
| 59 | + |
| 60 | +二叉搜索树的插入操作与二叉树的查找操作过程类似,具体步骤如下: |
| 61 | + |
| 62 | +1. 如果二叉搜索树为空,则创建一个值为 `val` 的节点,并将其作为二叉搜索树的根节点。 |
| 63 | +2. 如果二叉搜索树不为空,则将待插入的值 `val` 与二叉搜索树根节点的值 `root.val` 进行比较: |
| 64 | + 1. 如果 `val < root.val`,则递归将值为 `val` 的节点插入到左子树中。 |
| 65 | + 2. 如果 `val > root.val`,则递归将值为 `val` 的节点插入到右子树中。 |
| 66 | + |
| 67 | +### 3.2 二叉搜索树的插入代码实现 |
| 68 | + |
| 69 | +```Python |
| 70 | +class Solution: |
| 71 | + def insertIntoBST(self, root: TreeNode, val: int) -> TreeNode: |
| 72 | + if root == None: |
| 73 | + return TreeNode(val) |
| 74 | + |
| 75 | + if val < root.val: |
| 76 | + root.left = self.insertIntoBST(root.left, val) |
| 77 | + if val > root.val: |
| 78 | + root.right = self.insertIntoBST(root.right, val) |
| 79 | + return root |
| 80 | +``` |
| 81 | + |
| 82 | +## 4. 二叉搜索树的创建 |
| 83 | + |
| 84 | +> **二叉搜索树的创建**:根据数组序列中的元素值,建立一棵二叉搜索树。 |
| 85 | +
|
| 86 | +### 4.1 二叉搜索树的创建算法步骤 |
| 87 | + |
| 88 | +二叉搜索树的创建操作是从空树开始,按照给定数组元素的值,依次进行二叉搜索树的插入操作,最终得到一棵二叉搜索树。具体算法步骤如下: |
| 89 | + |
| 90 | +1. 初始化二叉搜索树为空树。 |
| 91 | +2. 遍历数组元素,将数组元素值 `nums[i]` 依次插入到二叉搜索树中。 |
| 92 | +3. 将数组中全部元素值插入到二叉搜索树中之后,返回二叉搜索树的根节点。 |
| 93 | + |
| 94 | +### 4.2 二叉搜索树的创建代码实现 |
| 95 | + |
| 96 | +```Python |
| 97 | +class Solution: |
| 98 | + def insertIntoBST(self, root: TreeNode, val: int) -> TreeNode: |
| 99 | + if root == None: |
| 100 | + return TreeNode(val) |
| 101 | + |
| 102 | + if val < root.val: |
| 103 | + root.left = self.insertIntoBST(root.left, val) |
| 104 | + if val > root.val: |
| 105 | + root.right = self.insertIntoBST(root.right, val) |
| 106 | + return root |
| 107 | + def buildBST(self, nums) -> TreeNode: |
| 108 | + root = TreeNode(val) |
| 109 | + for num in nums: |
| 110 | + self.insertIntoBST(root, num) |
| 111 | + return root |
| 112 | +``` |
| 113 | + |
| 114 | +## 5. 二叉搜索树的删除 |
| 115 | + |
| 116 | +> **二叉搜索树的删除**:在二叉搜索树中删除值为 `val` 的节点。 |
| 117 | +
|
| 118 | +### 5.1 二叉搜索树的删除算法步骤 |
| 119 | + |
| 120 | +在二叉搜索树中删除元素,首先要找到待删除节点,然后执行删除操作。根据待删除节点所在位置的不同,可以分为 `3` 种情况: |
| 121 | + |
| 122 | +1. 被删除节点的左子树为空。则令其右子树代替被删除节点的位置。 |
| 123 | +2. 被删除节点的右子树为空。则令其左子树代替被删除节点的位置。 |
| 124 | +3. 被删除节点的左右子树均不为空,则根据二叉搜索树的中序遍历有序性,删除该节点时,可以使用其直接前驱(或直接后继)代替被删除节点的位置。 |
| 125 | + |
| 126 | +- **直接前驱**:在中序遍历中,节点 `p` 的直接前驱为其左子树的最右侧的叶子节点。 |
| 127 | +- **直接后继**:在中序遍历中,节点 `p` 的直接后继为其右子树的最左侧的叶子节点。 |
| 128 | + |
| 129 | +二叉搜索树的删除算法步骤如下: |
| 130 | + |
| 131 | +1. 如果当前节点为空,则返回当前节点。 |
| 132 | +2. 如果当前节点值大于 `val`,则递归去左子树中搜索并删除,此时 `root.left` 也要跟着递归更新。 |
| 133 | +3. 如果当前节点值小于 `key`,则递归去右子树中搜索并删除,此时 `root.right` 也要跟着递归更新。 |
| 134 | +4. 如果当前节点值等于 `key`,则该节点就是待删除节点。 |
| 135 | + 1. 如果当前节点的左子树为空,则删除该节点之后,则右子树代替当前节点位置,返回右子树。 |
| 136 | + 2. 如果当前节点的右子树为空,则删除该节点之后,则左子树代替当前节点位置,返回左子树。 |
| 137 | + 3. 如果当前节点的左右子树都有,则将左子树转移到右子树最左侧的叶子节点位置上,然后右子树代替当前节点位置。 |
| 138 | + |
| 139 | +### 5.2 二叉搜索树的删除代码实现 |
| 140 | + |
| 141 | +```Python |
| 142 | +class Solution: |
| 143 | + def deleteNode(self, root: TreeNode, key: int) -> TreeNode: |
| 144 | + if not root: |
| 145 | + return root |
| 146 | + |
| 147 | + if root.val > key: |
| 148 | + root.left = self.deleteNode(root.left, key) |
| 149 | + return root |
| 150 | + elif root.val < key: |
| 151 | + root.right = self.deleteNode(root.right, key) |
| 152 | + return root |
| 153 | + else: |
| 154 | + if not root.left: |
| 155 | + return root.right |
| 156 | + elif not root.right: |
| 157 | + return root.left |
| 158 | + else: |
| 159 | + curr = root.right |
| 160 | + while curr.left: |
| 161 | + curr = curr.left |
| 162 | + curr.left = root.left |
| 163 | + return root.right |
| 164 | +``` |
| 165 | + |
| 166 | +## 参考资料 |
| 167 | + |
| 168 | +- 【书籍】算法训练营 陈小玉 著 |
| 169 | +- 【书籍】算法竞赛入门经典:训练指南 - 刘汝佳,陈锋 著 |
| 170 | +- 【书籍】算法竞赛进阶指南 - 李煜东 著 |
| 171 | + |
0 commit comments