Functor Hierarchy

It's just more and more ways to make a f a -> f b function:

Functor     <$> ::   (a -> b) -> (f a -> f b)
Applicative <*> :: f (a -> b) -> (f a -> f b)
Monad       =<< :: (a -> f b) -> (f a -> f b)

One thing that Applicative allows is mapping over multiple arguments, e.g.:

f t = t
g t = 1 - t
(*) <$> f :: Parametric (a -> a)
(*) <$> f <*> g :: Parametric a

(whereas with just map aka <$> there is no way to incorporate the second argument as in the final <*> step above)

Lines of Lines, Bézier Curves, and Haskell's Function Monad

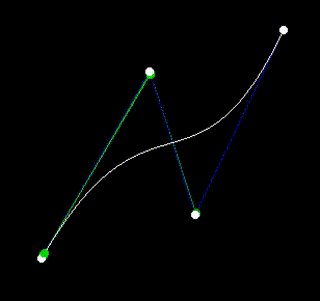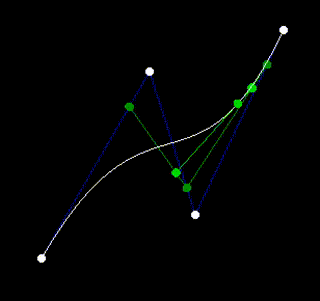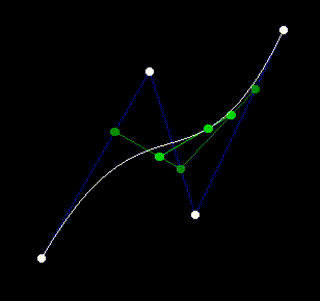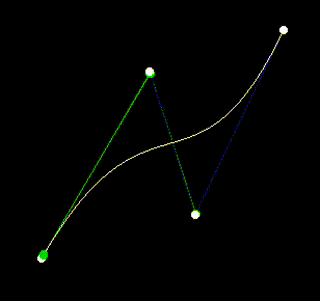
A line usually goes from one point to another, but can we draw a line from one line to another?

It turns out we can, and it's called a Bézier curve.

A Line Between Two Points

We'll start with the usual line between two points.

First we define the 1-dimensional line1d from a number a at time t=0 to a number b at t=1:

type Time = Float

line1d :: Float -> Float -> Time -> Float
line1d a b t = (1 - t)*a + t*b

Then the multi-dimensional line between two points p and q is the combination of the one-dimensional lines on each dimension:

type Point = [Float]

line :: Point -> Point -> Time -> Point
line p q t = [line1d a b t | (a, b) <- zip p q]

We can try it out in ghci and see if it works:

λ> let l = line [0, 0] [1, 2]
λ> l 0
[0, 0]
λ> l 1
[1, 2]
λ> l 0.5
[0.5, 1]

So far so good!

A Line Between Two Lines

Now we can see what a line between two lines looks like:

λ> let f = line [0, 0] [0, 1]
λ> let g = line [1, 0] [1, 1]
λ> let h t = line (f t) (g t) t
λ> h 0
[0, 0]
λ> h 1
[1, 1]
λ> h 0.5
-- TODO [x, y]

Cool!

A Line Between Multiple Points

If we have three points, we can draw two lines to connect them together.

λ> let points = [[0, 0], [1, 1], [1, 0]]
λ> let l01 = line points!!0 points!!1
λ> let l12 = line points!!1 points!!2

But we know how to make a line between two lines:

λ> let l02 t = line (l01 t) (l12 t) t

What if we have four points?

λ> let ps = [[0, 0], [0, 1], [1, 1], [1, 0]]

λ> let l01 = line ps!!0 ps!!1
λ> let l12 = line ps!!1 ps!!2
λ> let l23 = line ps!!2 ps!!3

λ> let l02 t = line (l01 t) (l12 t) t
λ> let l13 t = line (l12 t) (l23 t) t

λ> let l03 t = line (l02 t) (l13 t) t

Crazy! This is what a Bézier curve is.

We can generalize this process for any list of points, where the Bézier of a single point is fixed at that point, and the Bézier of n points is the line between the Bézier of the first n-1 points (init ps) and the Bézier of the last n-1 points (tail ps):

bezier :: [Point] -> Time -> Point
bezier [p] t = p
bezier ps  t = line (bezier (init ps) t) (bezier (tail ps) t) t

Now we can make crazy curves through a bunch of points:

λ> let f = bezier [[0, 0], [1, 1], [2, 0], [1, 0], [2, 1], [3, 0]]

The Function Monad

So far the code looks like this:

type Time = Float
type Point = [Float]

line1d :: Float -> Float -> Time -> Float
line1d a b t = (1 - t)*a + t*b

line :: Point -> Point -> Time -> Point
line p q t = [line1d a b t | (a, b) <- zip p q]

bezier :: [Point] -> Time -> Point
bezier [p] t = p
bezier ps  t = line (bezier (init ps) t) (bezier (tail ps) t) t

It's not terrible, but we end up referencing t a bunch of times, even though everything other than line1d just passes it along untouched.

Notice that the return type of all of our functions is a parametric function from time to some value. We can make this more apparent with a type alias type Parametric a = Time -> a.

It turns out Parametric is a monad—specifically the function monad, for passing around an implicit argument—so we can use Haskell's monadic do notation (remember: do no tation can do no harm) and its many monadic helper functions to get rid of most of the mentions of t:

The final implementation:

import Control.Monad (zipWithM)

type Parametric a = Float -> a
type Point = [Float]

line1d :: Float -> Float -> Parametric Float
line1d a b = \t -> (1 - t)*a + t*b

line :: Point -> Point -> Parametric Point
line p q = zipWithM line1d p q

bezier :: [Point] -> Parametric Point
bezier [p] = return p
bezier ps  = do p <- bezier (init ps)
                q <- bezier (tail ps)
                line p q

Both line and bezier are now point-free—i.e. they don't mention t at all—the monadic machinery implicitly passes the time argument along until it is needed.

line1d is unchanged because it's actually using the value of t, not just passing it along.

line looks clever thanks to the built-in zipWithM, but that's just equivalent to sequence $ zipWith line1d p q, which is equivalent to sequence [line1d a b | (a, b) <- zip p q], where sequence converts the list comprehension's [Parametric Float] to Parametric [Float], aka Parametric Point.

The base case of bezier is still just a constant function, but in the function monad that's equivalent to return, so we use return instead of const to keep things purely monadic, which lets us switch to a different monad if we want to, without changing any code.

A Different Monad

line and bezier are implemented in an entirely monad-independent way, which means we can change the underlying monad used in line1d without changing the code of bezier or line at all. Let's try it!

Suppose we want line1d to do nothing if t < 0 or t > 1. To accomplish this we can wrap our existing monad in the transformers library's MaybeT, a "monad transformer" wrapper turning Float -> Maybe a into one combined monad instead of two nested ones:

import Control.Monad.Trans.Maybe

type Parametric a = MaybeT ((->) Float) a

line1d :: Float -> Float -> Parametric Float
line1d a b = MaybeT go
  where go t | t >= 0 && t <= 1 = Just $ (1 - t)*a + t*b
             | otherwise = Nothing

The cool part is that we don't have to change the implementation of line or bezier at all.

We can try it out:

λ> let f = bezier [[0, 0], [1, 1], [2, 0], [1, 0], [2, 1], [3, 0]]
λ> runMaybeT f 1
Just [3, 0]
λ> runMaybeT f 10
Nothing

Applicative Functor Operators

Every monad is also an applicative functor, so just for fun, here's a completely equivalent way to write bezier using applicative functor operators:

bezier :: [Point] -> Parametric Point
bezier [p] = pure p
bezier ps  = join $ line <$> bezier (init ps) <*> bezier (tail ps)

The join is unfortunate, but is necessary because line takes two arguments, which doesn't play perfectly with the applicative machinery. The fact that we have to resort to join also shows that Parametric is more than just an applicative functor, since purely applicative functors can't be joined, only monadic ones can.

Speeding Things Up

For n points, the current algorithm recurses n times, branching into 2 calls at each step, which means it runs in exponential time!

When we look at a Bézier curve as the line between two other Bézier curves, it's not obvious how to avoid this.

However, splitting an n-point curve into two completely separate (n-1)-point curves ignores the fact that there is lots of overlap between those two curves. If instead we look at things in terms of lines, it becomes clear that at a fixed time any n-point curve can be reduced to an n-1 point curve, which it meets at that time.

This approach is called de Casteljau's algorithm, and takes us from exponential time down to quadratic time, which can be seen if you chart out the recursion in both approaches.

TODO Note that the quadratic algorithm is equivalent to memoization of the exponential algorithm.

bezier :: [Point] -> Parametric Point
bezier [p] = return p
bezier ps  = bezier =<< zipWithM line ps (tail ps)

Bezier.hs

A quick demonstration of how simple Bezier curves are, and how easily you can implement them in Haskell.

For example, to play with the Bezier curve on the four points of the unit square you would run:

> ghci Bezier.hs
>> let squareCurve = bezier [[0.0, 0.0], [0.0, 1.0], [1.0, 1.0], [1.0, 0.0]]

And then you can see where the curve is at various points along its path from t=0 to t=1:

>> squareCurve 0.0
  [0.0,0.0]
>> squareCurve 0.25
  [0.15625,0.5625]
>> squareCurve 0.5
  [0.5,0.75]
>> squareCurve 0.75
  [0.84375,0.5625]
>> squareCurve 1.0
  [1.0,0.0]

To run the graphical version, cabal install gloss (which may require brew install llvm first, I can't remember...) And then:

> ghc Bezier.hs Main.hs
> ./Main

Click to add a point, 'd' to delete it, space to pause, up and down to increase level of detail, and 'v' to toggle whether sub-curves are drawn.