-
Notifications
You must be signed in to change notification settings - Fork 40
Chapter 3. The H in HSM
In the last chapter, we learned how to use HSM to author flat state machines. Although HSM is perfectly suited to creating flat state machines, it's main feature is its built-in support for hierarchical state machines. In this chapter, we'll learn what is a hierarchical state machine, and how to author them with HSM.
The best way to understand why a hierarchical state machine is useful is with an example. Our example will be that of a typical state machine we'd build for a character controller in a video game. We first start out with a simple, flat state machine, much like the ones we saw in Chapter 2:
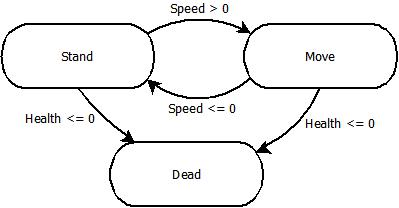
We have 3 states with certain transitions between them. Both Stand and Move can transition between each other, based on speed, and if the character's health drops to 0, in either state we make sure to go to Dead. Now let's add a few more states and transitions:
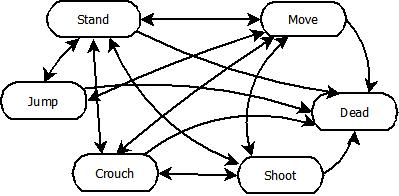
We've added 3 new states: Jump, Crouch, and Shoot. Although it looks like a big mess of arrows, if you look carefully, you will see that the transitions make sense: you can Jump, Crouch, or Shoot from both Stand and Move, and from all states, you must be able to go to Dead.
Now the fact that this looks like a big mess on a picture is not just because it's on a picture - this type of mess translates into code as well. If you've ever had to write a flat state machine in code that had more than just a few states, and many possible transitions, you've quickly learned how difficult it can be to manage. Indeed, it is very common for bugs to creep up at the 11th hour because you forgot a transition to a state from one that you never thought would require it.
The truth is, the complexity of a flat state machine is often exponentially proportional to the number of states it contains. When you add a new state, the number of transitions that need to be added increase as the state machine itself grows. For example, if we were to add a Hurt state to the above state machine, we'd need to add a transition to Hurt from all states except Dead.
The problem with flat state machines is that all states are treated as independent units: you can only be in one state at time. However, often it would make sense to be in more than one state at the same time. For example, let's say we introduce the state Alive to represent the opposite of Dead. Alive would transition to dead as long as health <= 0. Now logically, it makes sense to say that as long as you're in any of the states except for Dead in our example above, you should also be in Alive. Indeed, when you're standing, moving, crouching, and shooting, you're still alive, right?
Here's an example of what such a state machine could look like:
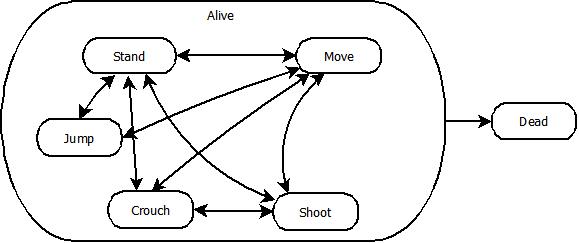
As you can see, most states have been grouped into the new Alive state, which is now the only one that transitions to the Dead state. This is exactly what a hierarchical state machine is: it provides a way of nesting states within other states.
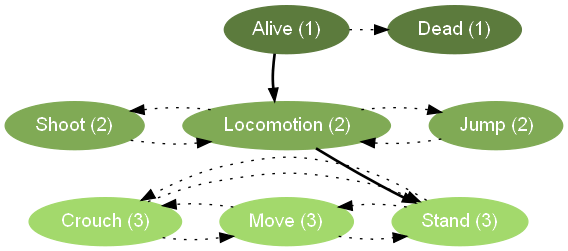
Here's another version of this HSM with some more state nesting:
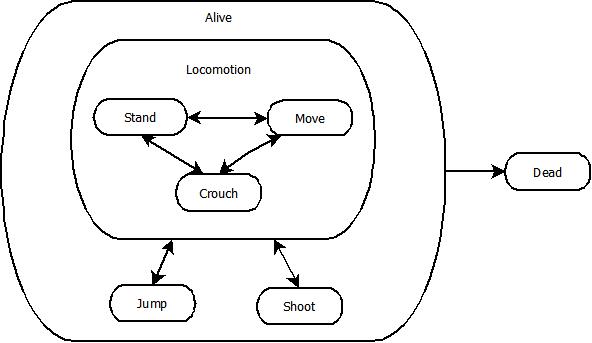
In this version, we've grouped Stand, Move, and Crouch into a Locomotion state, which is itself an inner state of Alive. Not only has the number of transitions greatly reduced, it's much easier to understand the state machine. For instance, we can see that whether you're standing, crouching, or moving, you can start shooting, but you can't shoot while jumping. Thus, by making our flat state machine a hierarchical one, we can more easily infer the rules of our character controller.
Hopefully by now you can see how useful hierarchical state machines can be. The rest of this chapter will delve into how to use HSM to implement these types of state machines.
The images in the previous section displayed state nesting as concentric circles. Although this is useful for understanding the concept of hierarchical state machines, it's not practical to draw them this way for larger state machines with many levels of nesting. The rest of this book uses the output from plotHsm, which takes a different approach to representing state hierarchies. For instance, this state machine:

... looks like this using plotHsm:
Here are some tips for understanding this output:
- The number in parentheses is the depth level of the state
- State colors are brighter for more deeply nested states
- Solid lines represent inner transitions (from an outer state to an inner state)
- Dotted lines represent sibling transitions
Finally, plotHsm will group states together into clusters based on the state name: if a set of states share the same prefix followed by an underscore in their name, they will be grouped together. For instance:
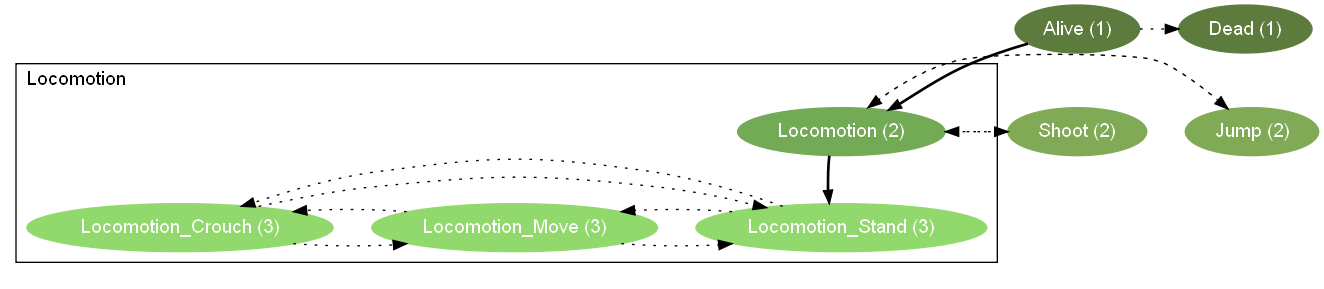
Because we've prefixed the state names for Crouch, Move, and Stand with "Locomotion_", plotHsm clusters the states into a box labelled "Locomotion". This can be especially useful in understanding larger state machines where you'll typically have many state clusters at the same depth level. Of course, it can be cumbersome to prefix all your state names this way, so we recommend doing it to group the deepest, or innermost, set of states.
When talking (or writing) about hierarchical state machines, the terms parent and child will often be used when describing the relationship between a state and its nested state. In HSM, we use the terms outer and inner instead. We do this to avoid confusion with the fact that states are actually C++ polymorphic classes, so a parent/child relationship already exists at the class hierarchy level (e.g. every state is a child class of hsm::State).
There are a few other terms we use to describe the relationships between states along with outer and inner: sibling, immediate, and root. The best way to define these is with an example:

We can describe the state relationships in the state machine above as follows:
- Shoot, Locomotion, Jump, Crouch, Move, and Stand are inner states of Alive
- Shoot, Locomotion, and Jump are inner states of Alive
- Shoot, Locomotion, and Jump are also immediate inner states of Alive
- Crouch, Move, and Stand are immediate inner states of Locomotion
- Alive is the outer state of Shoot, Locomotion, Jump, Crouch, Move, and Stand
- Alive is the immediate outer state of Shoot, Locomotion, and Jump
- Dead is not an outer state
- Alive and Dead are root states of the state machine
- Alive and Dead are sibling states
- Shoot, Locomotion, Jump are sibling states
- Crouch, Move, and Stand are sibling states
- If you're in the Move state, you're also in the Locomotion state and the Alive state
- If you're in the Shoot state, you're also in the Alive state
This is the terminology that is used throughout this book as well as in the HSM code.
Before we look at how to author hierarchical state machines, we must first discuss one of the key features of how HSM manages states: the state stack.
Each StateMachine instance manages a stack of States instances. The first state pushed onto the stack is the outermost state, the next state pushed is its inner, and the last state pushed is the innermost state. A sibling transition will first pop the current state from the stack, and then push the target state back onto the stack, thus keeping it at the same depth. Inner and inner entry transitions, which we'll cover in the next few sections, are used to push inner states onto the stack. Every time a state is pushed onto the stack, it's OnEnter gets called.
When a source state makes a sibling transition to a target state, the source state and its inners are all popped off the stack before the target state is pushed. This happens from innermost up to the source state, with OnExit being called on each state, giving each state a chance to clean itself up.
Let's take the example from the previous section. After running ProcessStateTransitions, the state stack might look like this:
| State Stack |
|---|
| Alive |
| Locomotion |
| Stand |
If the player presses the movement input, the next call to ProcessStateTransitions would result in this state stack:
| State Stack |
|---|
| Alive |
| Locomotion |
| Move |
In this case, Stand made a sibling transition to Move, resulting in Stand::OnExit (pop) followed by Move::OnEnter (push). Now, if the character is killed, the next call to ProcessStateTransitions would result in this state stack:
| State Stack |
|---|
| Dead |
This time, Alive made a sibling transition to Dead, resulting in Move::OnExit (pop), Locomotion::OnExit (pop), Alive::OnExit (pop), and finally Dead::OnEnter (push).
In the next couple of sections, we'll learn about the two types of transitions used to push inner states.
So far, the only type of transition we have seen is the sibling transition, which is used to exit a state and enter another state. In this section, we introduce the inner entry transition, which is used to enter a new inner state. Let's start with some code:
// inner_entry_transition.cpp
#include "hsm/statemachine.h"
using namespace hsm;
class MyOwner
{
public:
MyOwner();
void UpdateStateMachine();
void Die() { mDead = true; }
private:
bool IsDead() const { return mDead; }
bool PressedMove() const { return false; } // Stub
bool mDead;
friend struct MyStates;
StateMachine mStateMachine;
};
struct MyStates
{
struct BaseState : StateWithOwner<MyOwner>
{
};
struct Alive : BaseState
{
virtual Transition GetTransition()
{
if (Owner().IsDead())
return SiblingTransition<Dead>();
return InnerEntryTransition<Locomotion>();
}
};
struct Dead : BaseState
{
virtual Transition GetTransition()
{
return NoTransition();
}
};
struct Locomotion : BaseState
{
virtual Transition GetTransition()
{
return InnerEntryTransition<Stand>();
}
};
struct Stand : BaseState
{
virtual Transition GetTransition()
{
if (Owner().PressedMove())
return SiblingTransition<Move>();
return NoTransition();
}
};
struct Move : BaseState
{
virtual Transition GetTransition()
{
if (!Owner().PressedMove())
return SiblingTransition<Stand>();
return NoTransition();
}
};
};
MyOwner::MyOwner()
: mDead(false)
{
mStateMachine.Initialize<MyStates::Alive>(this);
mStateMachine.SetDebugInfo("TestHsm", TraceLevel::Basic);
}
void MyOwner::UpdateStateMachine()
{
mStateMachine.ProcessStateTransitions();
mStateMachine.UpdateStates();
}
int main()
{
MyOwner myOwner;
myOwner.UpdateStateMachine();
myOwner.Die();
myOwner.UpdateStateMachine();
}Before we talk about the code, let's take a look at the plotHsm output for this state machine:
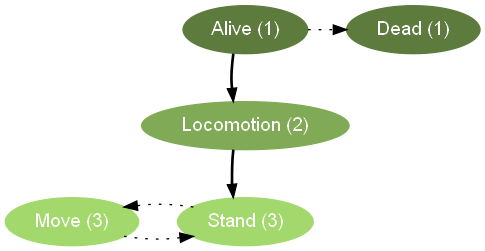
Looking at this image, we can see that Alive and Dead are siblings, and that Move and Stand are also siblings. Locomotion, however, is an inner state of Alive, and both Move and Stand are inner states of Locomotion.
Now notice that although both Stand and Move are inner states of Locomotion, there is only one arrow going from Locomotion to Stand, but none from Locomotion to Move. The reason for this is that Locomotion makes an inner entry transition to Stand. We can see this when looking at the code for state Locomotion:
struct Locomotion : BaseState
{
virtual Transition GetTransition()
{
return InnerEntryTransition<Stand>();
}
};When a state returns an InnerEntryTransition<TargetState>, the state machine will enter TargetState if no other inner state has been entered yet.
In other words, if a state at depth D on the state stack returns InnerEntryTransition<TargetState>, as long as there is no state yet at depth D+1, TargetState will be created and pushed onto the stack. The next time the same state returns InnerEntryTransition<TargetState>, because an inner state has already been pushed, this transition will be ignored.
Back to our example, Locomotion will always return InnerEntryTransition<Stand>() from its GetTransition function; but the inner transition will only happen the first time it's returned, at which point Stand will be created as an inner state. Now Stand is free to make sibling transitions:
struct Stand : BaseState
{
virtual Transition GetTransition()
{
if (Owner().PressedMove())
return SiblingTransition<Move>();
return NoTransition();
}
};We can see that if the user presses the move input, Stand will sibling to Move. When this occurs, Move will be the current inner state of Locomotion. Note that even though Locomotion::GetTransition will continue to return InnerEntryTransition<Stand>(), this will have no effect; Move will remain its current inner state.
As usual, we've set up the state machine to output basic level tracing:
mStateMachine.SetDebugInfo("TestHsm", TraceLevel::Basic);Which produces this output:
HSM_1_TestHsm: Init : struct MyStates::Alive
HSM_1_TestHsm: Entry : struct MyStates::Locomotion
HSM_1_TestHsm: Entry : struct MyStates::Stand
HSM_1_TestHsm: Sibling : struct MyStates::Dead
The first thing to note is that the output is indented with respect to the state depth on the stack. We can clearly see that Alive made an inner entry transition to Locomotion, and Locomotion also made an inner entry to Stand. Finally, we see that there was a sibling transition to Dead, and since it's indentation level matches that of Alive, we know that Alive must have made that transition.
The Alive to Dead sibling transition implies that Stand, Locomotion, and Alive were all popped from the stack (and OnExit called on each). If you wish to see this explicitly, you can change the trace level from Basic to Diagnostic as follows:
mStateMachine.SetDebugInfo("TestHsm", TraceLevel::Diagnostic);Now the output becomes:
HSM_1_TestHsm: Init : struct MyStates::Alive
HSM_1_TestHsm: Entry : struct MyStates::Locomotion
HSM_1_TestHsm: Entry : struct MyStates::Stand
HSM_2_TestHsm: Pop : struct MyStates::Stand
HSM_2_TestHsm: Pop : struct MyStates::Locomotion
HSM_2_TestHsm: Pop : struct MyStates::Alive
HSM_1_TestHsm: Sibling : struct MyStates::Dead
We now see three new "Pop" lines for Stand, Locomotion, and Alive. Although this is useful for understanding how the HSM works, once you're used to it, you can easily infer when states are popped, which is why these lines are not part of the Basic trace output.
In the previous section, we covered the InnerEntryTransition, which is used to push an inner state only if there is no inner state yet on the stack. The more generalized InnerTransition, on the other hand, is used to force an inner state onto the state stack, regardless of what's on it.
More specifically: when InnerTransition<TargetState> is returned from GetTransition, the state machine makes sure that TargetState becomes (or remains) the inner state. If there is no inner state yet, TargetState gets pushed. If the inner state is already TargetState, nothing happens. If the inner state is not TargetState, the current inner state - along with all its inners - are popped off the stack (from innermost out), and TargetState is then pushed.
Let's take a look at an example:
// inner_transition.cpp
#include "hsm/statemachine.h"
using namespace hsm;
class MyOwner
{
public:
MyOwner();
void UpdateStateMachine();
void Die() { mDead = true; }
void SetMove(bool enable) { mMove = enable; }
private:
bool IsDead() const { return mDead; }
bool PressedMove() const { return mMove; }
bool mDead;
bool mMove;
friend struct MyStates;
StateMachine mStateMachine;
};
struct MyStates
{
struct BaseState : StateWithOwner<MyOwner>
{
};
struct Alive : BaseState
{
virtual Transition GetTransition()
{
if (Owner().IsDead())
return SiblingTransition<Dead>();
return InnerEntryTransition<Locomotion>();
}
};
struct Dead : BaseState
{
virtual Transition GetTransition()
{
return NoTransition();
}
};
struct Locomotion : BaseState
{
virtual Transition GetTransition()
{
if (Owner().PressedMove())
return InnerTransition<Move>();
else
return InnerTransition<Stand>();
}
};
struct Stand : BaseState
{
};
struct Move : BaseState
{
};
};
MyOwner::MyOwner()
: mDead(false)
, mMove(false)
{
mStateMachine.Initialize<MyStates::Alive>(this);
mStateMachine.SetDebugInfo("TestHsm", TraceLevel::Basic);
}
void MyOwner::UpdateStateMachine()
{
mStateMachine.ProcessStateTransitions();
mStateMachine.UpdateStates();
}
int main()
{
MyOwner myOwner;
myOwner.UpdateStateMachine();
printf("Set Move = true\n");
myOwner.SetMove(true);
myOwner.UpdateStateMachine();
printf("Set Move = false\n");
myOwner.SetMove(false);
myOwner.UpdateStateMachine();
}This example is the same as the one from the InnerEntryTransition section, except we've modified how the Stand and Move states are transitioned to. In the previous section, Locomotion made an InnerEntryTransition to Stand, and then Stand and Move would sibling to each other based on the result of Owner().PressedMove():
struct Locomotion : BaseState
{
virtual Transition GetTransition()
{
return InnerEntryTransition<Stand>();
}
};
struct Stand : BaseState
{
virtual Transition GetTransition()
{
if (Owner().PressedMove())
return SiblingTransition<Move>();
return NoTransition();
}
};
struct Move : BaseState
{
virtual Transition GetTransition()
{
if (!Owner().PressedMove())
return SiblingTransition<Stand>();
return NoTransition();
}
};In the current example, Locomotion uses InnerTransition to select which inner state will be pushed on the stack:
struct Locomotion : BaseState
{
virtual Transition GetTransition()
{
if (Owner().PressedMove())
return InnerTransition<Move>();
else
return InnerTransition<Stand>();
}
};
struct Stand : BaseState
{
};
struct Move : BaseState
{
};The main difference is that Locomotion decides whether Stand or Move should be the current inner state by using InnerTransition. Formerly, Locomotion only decided which of these states to start in - Stand in our case - by returning an InnerEntryTransition to that state; afterwards, Stand and Move used SiblingTransitions to decide which state should be the current inner of Locomotion.
In main, we toggle the 'move' variable to see these inner transitions in action:
int main()
{
MyOwner myOwner;
myOwner.UpdateStateMachine();
printf("Set Move = true\n");
myOwner.SetMove(true);
myOwner.UpdateStateMachine();
printf("Set Move = false\n");
myOwner.SetMove(false);
myOwner.UpdateStateMachine();
}This produces the following output:
HSM_1_TestHsm: Init : struct MyStates::Alive
HSM_1_TestHsm: Entry : struct MyStates::Locomotion
HSM_1_TestHsm: Inner : struct MyStates::Stand
Set Move = true
HSM_1_TestHsm: Inner : struct MyStates::Move
Set Move = false
HSM_1_TestHsm: Inner : struct MyStates::Stand
We can see from this output that Locomotion first makes an InnerTransition to Stand, then after we set the move field to true, Locomotion "inners" to Move, and finally after resetting the move field, Locomotion inners back to Stand.
The plotHsm output for this example is a little different from the last one:
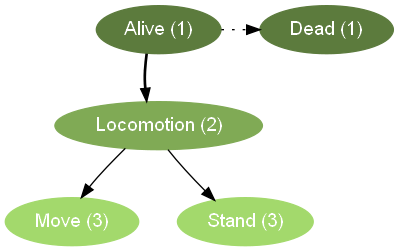
There are now two arrows indicating InnerTransitions from Locomotion to Move and Stand. Note that the InnerEntryTransition arrow from Alive to Locomotion is thicker than the InnerTransition arrows from Locomotion to Move and Stand.
When implementing state machines, there are many instances in which you need to query the current state stack. In this section, we'll take a look at the functions HSM provides for this purpose.
The most basic query is "are we in a given state?". For this, use StateMachine::IsInState<StateType>, which returns true if StateType is anywhere on the state stack. For instance, given the following state stack:
| State Stack |
|---|
| Alive |
| Locomotion |
| Stand |
Then mStateMachine.IsInState<Alive>();, mStateMachine.IsInState<Locomotion>(), and mStateMachine.IsInState<Stand>() would all return true, but mStateMachine.IsInState<Move>() would return false.
Another useful query function is StateMachine::GetState<StateType>, which returns a pointer to StateType if StateType is found on the stack, otherwise it returns NULL. This allows you to both check if you are in a given state and access members on that state, which means you can keep state-specific functions and data scoped to the state itself.
That covers the query functions available on the StateMachine class, but there are more available from the State class that can be used from within states (typically from GetTransition):
-
State::GetState<StateType> simply forwards to the same functions on the StateMachine class. This function can be useful when a state is interested in knowing whether a specific state is anywhere on the stack. However, the functions described below narrow the search direction, and are typically more useful and optimal.
-
State::GetOuterState<StateType> is similar to GetState except it searches the state stack starting from the current state's immediate outer to the outermost. This function is typically used when inner states need to access members from a common outer state.
-
State::GetInnerState<StateType> is similar to GetState except it searches the state stack from the current state's immediate inner to the innermost. This function is typically used when a state needs to make a sibling transition based on the existence of an inner state on the stack.
-
State::GetImmediateInnerState<StateType> is similar to GetInnerState, except it only checks for the existence of StateType at the current state's depth + 1 on the stack. This is useful when you know the target state is an immediate inner, and is mostly an optimization over GetInnerState as it doesn't search all inners.
Finally, State provides analogues to the above functions that check for the existence of a state: IsInState, IsInOuterState, IsInInnerState, and IsInImmediateInnerState.
We will see these state stack query functions in action in future examples.
In Chapter 2, we covered the basics of the StateMachine::ProcessStateTransitions function, but only to the extent of how it behaves with non-hierarchical (flat) state machines. In this section, we present the complete algorithm that takes into account the state stack, as well as InnerEntry and Inner transitions.
Note that this is perhaps the most important section in this book as it details the execution model of HSM. To build effective state machines, it is important to understand how states are created/destroyed, and how transitions are processed.
In Chapter 2, we presented the following pseudo-code to explain how StateMachine::ProcessStateTransitions works:
done = false
while (!done)
transition = currState.GetTransition()
if (transition != NoTransition)
currState.OnExit()
currState = transition.GetTargetState()
currState.OnEnter()
else
done = true
This pseudo-code was enough to understand how HSM processes non-hierarchical (flat) state machines. We now expand this code to see how it handles hierarchical state machines:
function ProcessStateTransitions
{
if stateStack.IsEmpty()
CreateAndPushInitialState()
bool stackModified = true
while (stackModified)
{
stackModified = ProcessStateTransitionsOnce()
}
}
function ProcessStateTransitionsOnce
{
for (depth = 0; depth < stateStack.size(); ++depth)
{
State* currState = GetStateAtDepth(depth)
Transition transition = currState->GetTransition()
if transition.Type() == NoTransition
{
continue // Move to next inner
}
else if transition.Type() == Inner
{
if transition.TargetState() == GetStateAtDepth(depth + 1)
{
continue // Inner is already target state, move to next inner
}
else
{
// Pop all states under us and push target
PopStatesToDepth(depth + 1) // Invokes OnExit on each state, then pops
PushState(CreateState(transition.TargetState())) // Pushes to stack, then calls OnEnter
return true // State stack was modified
}
}
else if transition.Type() == InnerEntry
{
// If current state has no inner (is currently the innermost), then push the entry state
if GetStateAtDepth(depth + 1) == NULL
{
State* targetState = CreateState(transition.TargetState())
PushState(targetState) // Pushes to stack, then calls OnEnter
return true // State stack was modified
}
}
else if transition.Type() == Sibling
{
// Pop all states under and including current, then push target state
PopStatesToDepth(depth)
State* targetState = CreateState(transition)
PushState(targetState) // Pushes to stack, then calls OnEnter
return true // State stack was modified
}
}
return false // State stack was not modified
}
This version of ProcessStateTransitions is certainly longer than the one we presented in Chapter 2. However, it should be fairly straightforward, and it's the same code you'll find in the StateMachine implementation, only simplified to help focus on the important parts.
The first thing you'll probably notice is that the process is broken down into two functions. We'll begin by focusing on ProcessStateTransitionsOnce. This function's role is to process each state on the stack from outermost (at depth 0) to innermost, invoking GetTransition on each state, and as soon as a state returns a transition that would modify the state stack, it performs the transition and returns true to signal that a modification was made. If no state returns a transition that would modify the current state stack, the function returns false to signal that no modification was made.
For each transition type, we can see how the state stack is manipulated. There should be no surprises here; how the stack is manipulated corresponds to how each transition was defined earlier in this chapter. Note that Sibling transitions always modify the state stack, while InnerEntry transitions only modify the stack if there's no inner state yet, and Inner transitions only modify the stack when the current inner state is not already the target state.
Now keeping in mind that ProcessStateTransitionsOnce returns whether or not the state stack was modified, ProcessStateTransition simply calls ProcessStateTransitionsOnce in a loop until the latter returns false. Effectively, ProcessStateTransition's role is to keep processing state transitions on the stack from outermost to innermost (via ProcessStateTransitionsOnce) until there are no more transitions that modify the stack. When this happens, we say that the state stack has settled.
Let's talk about the rationale behind some of the decisions in the ProcessStateTransition algorithm.
First, why does ProcessStateTransition need to keep iterating over the state stack until the stack has settled? Why not simply run through the stack once by just calling ProcessStateTransitionOnce one time? The main reason is idempotence: all things being equal, if you call StateMachine::ProcessStateTransitions twice, the second call should effectively be a "no-op" (i.e. should not modify the state stack).
To understand why this is important, let's say in a game, an enemy deals damage to the player, dropping his health value to 0. Depending on how the state machine was designed, it is possible that it would need to process its transitions from outer to inner more than once to get itself into the Dead state. If we did not make sure to keep processing transitions until the state stack is settled, then for one or more frames, the player would have a health value of 0, but would not be in the Dead state. This type of inconsistency usually results in bugs that are difficult to understand. In effect, what we want is a 1:1 mapping between external data and the state stack: if health is 0, we should be in the Dead state after calling ProcessStateTransitions.
NOTE: The fact that ProcessStateTransitions works this way is also useful in that it allows for transitions to so-called "transient" states: a state that will never exist on the stack once it has settled. A typical example is a "done" state, which is covered in Chapter 4
Another question that is often asked about the ProcessStateTransition algorithm is: why are transitions processed from outer to inner, rather than from inner to outer? The reason has to do with how a hierarchical state machine is typically organized: an outer state represents a more global state, while an inner states represent a more local state. Outer states make "bigger" - or more important - decisions than inner states, so they are processed first - they have priority. For instance, in most of our examples in this chapter, Alive is an outermost state, and no matter what inner states are currently on the stack, Alive will always sibling to Dead if health drops to 0. This transition is a high-priority transition, and thus is processed before inner transitions.
Let's discuss some of the important implications of how the ProcessStateTransitions algorithm keeps processing transitions until the state stack has settled.
First of all, keep in mind that State::GetTransition can be called more than once on any given state during a single call to StateMachine::ProcessStateTransitions. As a result, GetTransition is not a good place to execute "update" logic - for that, use the State::Update function instead, which is guaranteed to only get called once on each state. GetTransition should really only return what transition to make by reading/polling state data. In other words, GetTransition should generally have no side-effects apart from returning a transition that modifies the state stack.
Secondly, it's possible for ProcessStateTransitions to end up in an infinite transition loop - one where the state stack never settles. A simple example is one where state A siblings to B if boolean variable foo is true, and B siblings to A is foo is false. Fortunately, infinite transition loops like these are detected and reported by HSM via an assertion, and with the help of the trace output, are usually easy enough to understand and correct. (See the section on Deferred Transitions for one way to break such infinite transition loops).
In Chapter 2, we learned that StateMachine::UpdateStates can be used to invoke State::Update on the current state in a flat state machine. More generally, what StateMachine::UpdateStates actually does is invoke State::Update on each state on the state stack from outermost to innermost.
Let's take a look at an example of how UpdateStates works:
// revisit_update_states.cpp
#include "hsm/statemachine.h"
using namespace hsm;
class MyOwner
{
public:
MyOwner();
void UpdateStateMachine();
private:
friend struct MyStates;
StateMachine mStateMachine;
};
struct MyStates
{
struct BaseState : StateWithOwner<MyOwner>
{
};
struct A : BaseState
{
virtual Transition GetTransition()
{
return InnerEntryTransition<B>();
}
virtual void Update()
{
printf("A::Update\n");
}
};
struct B : BaseState
{
virtual Transition GetTransition()
{
return InnerEntryTransition<C>();
}
virtual void Update()
{
printf("B::Update\n");
}
};
struct C : BaseState
{
virtual Transition GetTransition()
{
return InnerEntryTransition<D>();
}
virtual void Update()
{
printf("C::Update\n");
}
};
struct D : BaseState
{
virtual void Update()
{
printf("D::Update\n");
}
};
};
MyOwner::MyOwner()
{
mStateMachine.Initialize<MyStates::A>(this);
mStateMachine.SetDebugInfo("TestHsm", TraceLevel::Basic);
}
void MyOwner::UpdateStateMachine()
{
mStateMachine.ProcessStateTransitions();
mStateMachine.UpdateStates();
}
int main()
{
MyOwner myOwner;
myOwner.UpdateStateMachine();
}Here's the output from this example:
HSM_1_TestHsm: Init : struct MyStates::A
HSM_1_TestHsm: Entry : struct MyStates::B
HSM_1_TestHsm: Entry : struct MyStates::C
HSM_1_TestHsm: Entry : struct MyStates::D
A::Update
B::Update
C::Update
D::Update
From this output, we can clearly see that Update gets called from outermost to innermost.
The State::Update function is where a state should perform whatever actions are relevant to that state. In the context of a hierarchical state machine, this allows you to encapsulate a state's behaviour where it belongs - in the state itself.
Also keep in mind that StateMachine::UpdateStates is invoked after StateMachine::ProcessStateTransitions, which means that State::Update is only called on states once the stack has settled. This means it's possible for certain states to never have State::Update called on them, even if transitioned to. For example, if A transitions to state B, and B immediately returns a sibling transition to state C, B::Update won't get called.
It's also worth noting that unlike State::Update, State::OnEnter and State::OnExit are always called on states that are transitioned to, so these are good functions to use if a state must always perform an action, regardless of whether they remain on the state stack at the end of StateMachine::ProcessTransitions.