This project is a minimal AMM (Automated Market Maker), inspired by Uniswap V2. It supports adding liquidity, quoting prices, and swapping ETH ↔ Token.
Deploy address https://sepolia.etherscan.io/address/0x4e6037b6613dba5aba761e3b14c7954f114947b7
src/UniswapV2.sol: Main contract implementing the AMM logiclib/openzeppelin-contracts/: ERC20 standard contract dependencytest/: Test scripts and casesscript/: Deployment scripts
Core invariant:
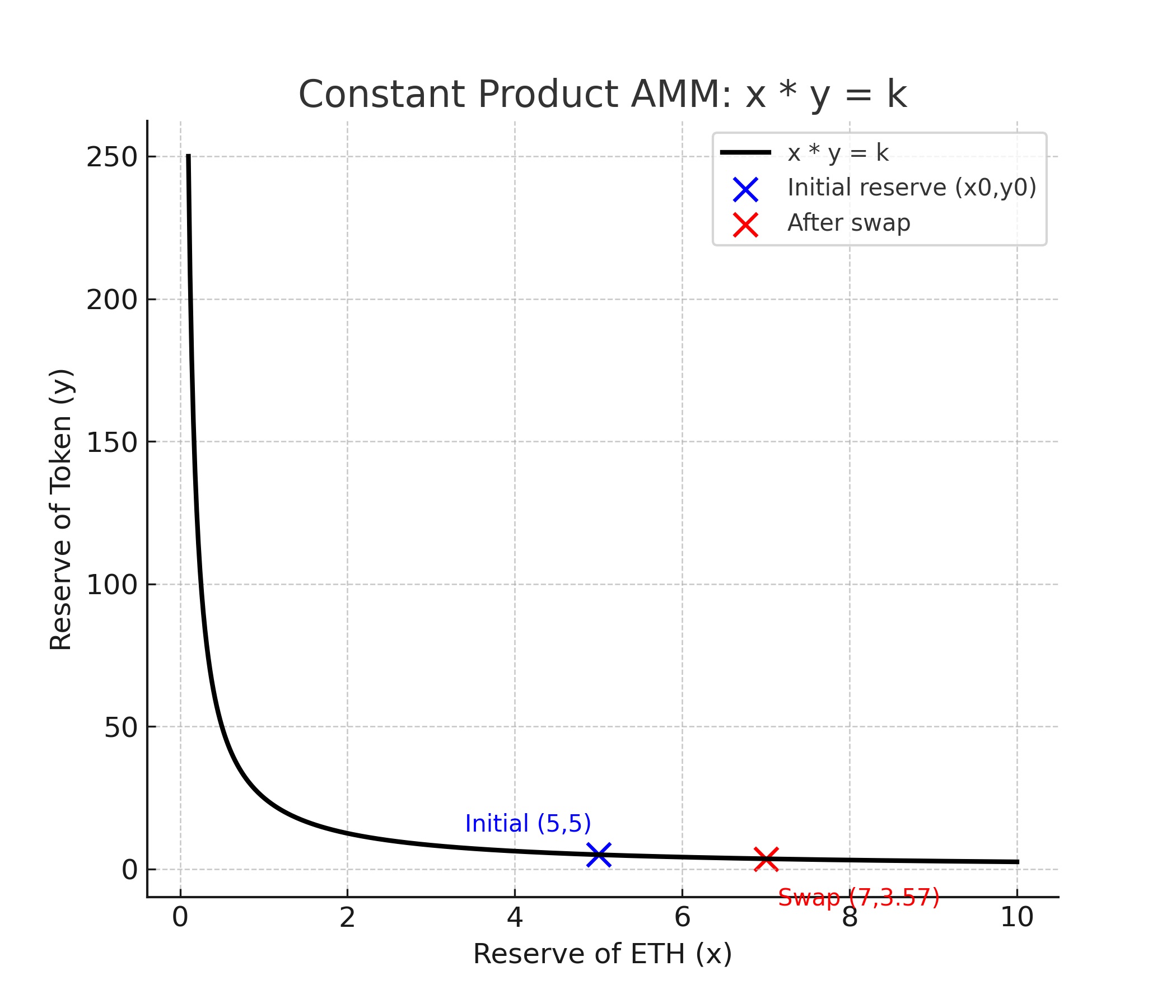
x * y = k
x= ETH reservey= Token reservek= Constant (liquidity invariant)
IERC20 public immutable token;
uint256 public reserveEth;
uint256 public reserveToken;token: ERC20 token contractreserveEth: ETH liquidity storedreserveToken: Token liquidity stored
👉 These reserves are always synced with the actual contract balances.
function addLiquidity(uint256 tokenAmount) external payable- User sends ETH + Tokens
- Both are deposited into the pool
- Internal reserves are updated via
_sync()
📌 Check: Zero liquidity is rejected.
function quote(uint256 amountIn, bool ethToToken)Formula (with 0.3% fee):
amountOut = (amountIn * 997 * reserveOut)
/ (reserveIn * 1000 + amountIn * 997)
- Preserves
x * y = k - Larger trades = higher slippage
function swapEthForToken() external payableSteps:
- User sends ETH (
msg.value) - Contract calculates
tokenOut = quote(ethIn, true) - Transfer Tokens to user
- Sync reserves
function swapTokenForEth(uint256 tokenIn) externalSteps:
- User sends Tokens via
transferFrom - Contract calculates ETH out using
quote - Contract sends ETH (
.call{value: ethOut}) - Sync reserves
The constant product formula produces a hyperbolic curve:
- Adding ETH decreases available Token (and vice versa)
- Prevents draining the pool completely
- Defines price slippage
Covered cases:
- ✅ Add liquidity success & revert on zero input
- ✅ Quote matches Uniswap V2 formula
- ✅ Swap ETH→Token & Token→ETH
- ✅ Reverts on insufficient liquidity
Run tests:
forge test -vvDeploy on Sepolia testnet:
forge script script/Deploy.s.sol:DeployExchange \
--rpc-url $SEPOLIA_RPC \
--broadcast- Simple AMM = no order book, only liquidity pool
- Core invariant = x * y = k
- Prices adjust automatically → slippage is inevitable
- Liquidity providers earn fees from swaps