canvas 实现事件系统

[wzf1997]

前言

大家好！ 我是热爱图形的fly, 之前在群里和粉丝讨论canvas 如何事件系统， 然后呢？ 我自己其实也对这个比较感兴趣， 我看过很多canvas 实现的项目， 比如canvas 实现思维导图 xmind ， canvas 实现一个绘图工具。 然后呢无论是哪一个，其实背后都是在canavs 背后实现了一套事件系统，可惜这些源码都不开源。所以本着学习的激情， 我参考了一些文章实现一个简单事件系统。本篇文章你可以学到下面👇这些内容

1. 我是怎么基于canvas去构建基础框架的
2. 几何算法—— 判断点是不是任意多边形内部
3. 如何进行事件分发和阻止事件冒泡

本篇文章我全是干货。欢迎点赞、关注、收藏。

基础框架的搭建

图形类

第一步我要做的事就是进行概念抽象，大家去想一下，canvas本质是一层画布，然后画布上很多图形，有长方形、圆形、以及任意闭合的多边形. 从面向对象的角度考虑的话， 我们可以封装一个基类 —— shape 每个图形是不是都在canvas 去显示，所以都应该有一个

draw 方法， 还有一个方法就是判断鼠标的点 是不是在当前图形的内部，这个我我们后面在讨论吧。 然后每个图形有自己的特有的属性，结合canvas 的api 去设置。

export class Circle extends Shape {
  constructor(props) {
    super()
    this.props = props
  }

  draw(ctx) {
  }

  // 判断鼠标的点是否在图形内部
  isPointInClosedRegion(mouse) {
  }
}

export class Rect extends Shape {
  constructor(props) {
    super()
    this.props = props
  }
  draw(ctx) {
  }

  // 判断鼠标的点是否在图形内部
  isPointInClosedRegion(mouse) {
  }
}

上面两个图形看结构都是一样的，不一样的draw方法, 我给你1分钟时间思考🤔下，canvas 是如何画矩形和画圆的。 其实 就是两个api一个 arc一个rect 然后 你传入对应的参数就好了。这里没什么， 不知道的同学可以去MDN去看下， 我已经讲了很多篇了。我就直接给出代码：

const { center, radius, fillColor = 'black' } = this.props
const { x, y } = center
ctx.save()
ctx.beginPath()
ctx.fillStyle = fillColor
ctx.arc(x, y, radius, 0, Math.PI * 2)
ctx.fill()
ctx.closePath()
ctx.restore()

这是圆的， save 和 restore 的方法 妙处 就是 比如我给圆设置红色 ，如果我再去画矩形， 矩形也会变成红色， 这样就不可控了，圆的话就是 圆心 加 半径，加填充颜色。

看完圆的我们在看下矩形的。

const { leftTop, width, height, fillColor = 'black' } = this.props
const { x, y } = leftTop
ctx.save()
ctx.beginPath()
ctx.fillStyle = fillColor
ctx.fillRect(x, y, width, height)
ctx.closePath()
ctx.restore()

矩形的属性 一个左上角的点一个长度，一个宽度。ok ,到这里图形基本搭建完成，下面开始搭建画布类

画布类

画布类的目前做的事情非常简单哈，初始化一些属性。首先他有个add() 方法，去往画布增加各个图形。增加的图形，每一个图形内部都去实现了draw 方法。这样实现了往canvas 加图形的操作哈。直接看代码：

// 新建一个画布类
export class Canvas {
  constructor() {
    this.canvas = document.getElementById('canvas')
    this.ctx = this.canvas.getContext('2d')
    this.allShapes = []
  }

  add(shape) {
    shape.draw(this.ctx)
    this.allShapes.push(shape)
  }
}

是不是很简单，我们写一些代码测试下：

const canvas = new Canvas()
const circle = new Circle({
  center: new Point2d(50, 50),
  radius: 50,
  fillColor: 'green',
})
const rect = new Rect({
  leftTop: new Point2d(50, 50),
  width: 100,
  height: 100,
  fillColor: 'black',
})
// 添加
canvas.add(circle)
canvas.add(rect)

这样写代码是不是感觉十分的舒服， 很清除， 可读性非常的高哇

OK，看来我们写的代码是没有问题的，下面写一个稍微复杂的图形，任意点组成的闭合polygon

polygon类

同样是也是有draw 和 isPointInClosedRegion 这个两个方法， 画图的这个方法呢， 属性就是一堆2d点， 第一个点是移动画笔🖌， 其余的点调用canvas lineTo的方法。 然后 闭合区域就好了 。

export class Polygon extends Shape {
  constructor(props) {
    super()
    this.props = props
  }
  draw(ctx) {
    const { points, fillColor = 'black' } = this.props
    ctx.save()
    ctx.beginPath()
    ctx.fillStyle = fillColor
    points.forEach((point, index) => {
      const { x, y } = point
      if (index === 0) {
        ctx.moveTo(x, y)
      } else {
        ctx.lineTo(x, y)
      }
    })
    ctx.fill()
    ctx.closePath()
    ctx.restore()
  }

  getDispersed() {
    return this.props.points
  }

  isPointInClosedRegion(event) {
  }
}

测试的话，我是随机在画布取了5个点， 我用了我之前写的Point2d类， 上有个random方法， 传入canvas 的长度和宽度。不清楚的同学看看我之前写 canvas实现点的移动， 那里 我有详细介绍过。测试代码如下:

const points = []
for (let i = 0; i < 5; i++) {
  points.push(Point2d.random(800, 600))
}
const shape = new Polygon({
  points,
  fillColor: 'orange',
})
// 添加到画布中
canvas.add(shape)

我们看下结果：

基类shape

写到这里就有人问到， 这个三个类 都继承 基类 shape, shape 有什么通用的能力呢？ 这里开始到我们本文的主题了， 就是每个图形的是不是有监听事件， 事件有很多种类型。每个类型下肯定有一大堆的监听函数， OK ，首先这是大家通用的能力， 或者是大家都需要的额东西， 我们就把放在基类中就好了， 那么我们用什么数据结构去存储呢—— 这种key Value 一看就是用Map, 行吧我们看下代码吧：

// 图形的基类
export class Shape {
  constructor() {
    this.listenerMap = new Map()
  }
  on(eventName, listener) {
    if (this.listenerMap.has(eventName)) {
      this.listenerMap.get(eventName).push(listener)
    } else {
      this.listenerMap.set(eventName, [listener])
    }
  }
}

On 这个方法哈， 第一个参数是事件名字， 第二个参数就是listener了， OK到目前为止， 每个图形对应的事件，都有了listener。

事件分发

这个小节，就是将所有canvas 绑定的事件，传递到每个图形上去。第一步哈，我们首先为canvas 绑定监听函数。

小Tips： 为canvas 增加键盘事件的时候，需要给canvas 增加一个属性 tabinex = 0 , 不然 绑定无效。

this.canvas.addEventListener(move, this.handleEvent(move))this.canvas.addEventListener(click, this.handleEvent(click))

Move 和click 是我定义个两个常量哈：

export const move = 'mousemove'export const click = 'mousedown'

handleEvent 这个方法 用到了函数式编程， 将事件名字 和逻辑 进行解耦哇。

handleEvent = (name) => (event) => {    this.allShapes.forEach((shape) => {      // 获取当前事件的所有监听者      const listerns = shape.listenerMap.get(name)      if ( listerns ) {        listerns.forEach((listener) => listener(event))      }    })  }

这样其实就实现了事件的分发，我们来测试下：

circle.on(click, (event) => {  //event.isStopBubble = true  console.log(event, 'circle')})rect.on(click, (event) => {  console.log(event, 'rect')})

不知道大家有没有发现问题， 虽然我们实现了事件分发，但是存在一个问题，我在画布上任意一点击， 都会触发，可能其实我点击的根本不在我画的图形内部。所以我们进行事件分发的时候，还要判断下鼠标的点 是不是在闭合的区域内部。所以说呢，每一个shape 内部都要去实现 isPointInClosedRegion 这个方法。

圆的实现

判断一个点是不是在于圆内，这个其实很简单，主要去比较 鼠标的点 和圆心的距离 与 半径做比较，然后就可以判断了哈， 这个没什么。直接上代码：

const { center, radius } = this.propsreturn mouse.point.distance(center) <= radius * radius

矩形的实现

判断一个点是不是在矩形内， 这里其实有个包围盒的概念，但是矩形 本来就是方方正正的，所以第一部根据， 左上角的点，算出矩形的minX， minY, maxX,maxY 然后 去拿鼠标的点去比较就好了。 这里我给大家画个图：

看到这张图应该不用说什么了， 直接上代码：

  // 判断鼠标的点是否在图形内部  isPointInClosedRegion(mouse) {    const { x, y } = mouse.point    const { leftTop, width, height } = this.props    const { x: minX, y: minY } = leftTop    const maxX = minX + width    const maxY = minY + height    if (x >= minX && x <= maxX && y >= minY && y <= maxY) {      return true    }    return false  }

点在任意多边形内（算法）

简单的图形我们可以通过一个数学关系去比较，但是复杂的多边形呢， 多边形分为 凹多边形 和凸多边形。那我们该怎么去解决呢？社区有下面几种方法：

1. 引射线法：从目标点出发引一条射线，看这条射线和多边形所有边的交点数目。如果有奇数个交点，则说明在内部，如果有偶数个交点，则说明在外部。
2. 面积和判别法：判断目标点与多边形的每条边组成的三角形面积和是否等于该多边形，相等则在多边形内部。

具体做法：将测试点的Y坐标与多边形的每一个点进行比较，会得到一个测试点所在的行与多边形边的交点的列表。在下图的这个例子中有8条边与测试点所在的行相交，而有6条边没有相交。如果测试点的两边点的个数都是奇数个则该测试点在多边形内，否则在多边形外。在这个例子中测试点的左边有5个交点，右边有三个交点，它们都是奇数，所以点在多边形内。

这里有人会问为什么奇数是在内部， 偶数是在外部呢？

我以最简单的例子，带你去解释为什么？这时候又到了， 画图时刻：

我们先从内部选一个点，然后向任意方向发出一条射线。 你会发现一个问题，我们射线第一次与直线相交 叫做 穿入， 后面再相交 叫做穿出， 你会发现内部的最后永远是穿入，没有穿出， 但是外部的点， 永远穿入的同时， 然后穿出。最后永远是穿出

算法实现

这里涉及到一个主要的算法就是 线段 和线段求焦点。我们新建一个Seg2d的类 线段肯定是有两个端点：

export class Seg2d {  constructor(start, end) {    this.endPoints = [start, end]    this._asVector = undefined  }  get start() {    return this.endPoints[0]  }  get end() {    return this.endPoints[1]  }  reverse() {    return new Seg2d(this.end.clone(), this.start.clone())  }  clone() {    return new Seg2d(this.start.clone(), this.end.clone())  }  get asVector() {    return (      this._asVector ||      (this._asVector = new Point2d(        this.endPoints[1].x - this.endPoints[0].x,        this.endPoints[1].y - this.endPoints[0].y      ))    )  }}

这都是基本操作没什么好讲的， 主要在类上 实现了 两个静态方法

1. 多个点转成线段
2. 线段和线段相交

我先来讲第一个，因为我们我们传给任意多边形的就是 点的集合， 所以，我们得将这些点连成线段组成闭合区域。

 //一堆点 获得闭合一堆线段  static getSegments(points, closed = false) {    const list = []    for (let i = 1; i < points.length; i++) {      list.push(new Seg2d(points[i - 1], points[i]))    }    if (closed && !points[0].equal(points[points.length - 1])) {      list.push(new Seg2d(points[points.length - 1], points[0]))    }    return list  }

Closed 这个参数， 因为区域是满足一个方向的。所以闭合区域 肯定是首尾相连的。

线段和线段求焦点

1. 列方程求两个直线的焦点
2. 判断每一条线段的两个端点是否都在另一条线段的两侧, 是则求出两条线段所在直线的交点, 否则不相交.

这里我们用第二种方法去实现 ：

第一步判断两个点是否在某条线段的两侧, 通常可采用投影法:

求出线段的法线向量, 然后把点投影到法线上, 最后根据投影的位置来判断点和线段的关系. 见下图

点a和点b在线段cd法线上的投影如图所示, 这时候我们还要做一次线段cd在自己法线上的投影(选择点c或点d中的一个即可).
主要用来做参考.
图中点a投影和点b投影在点c投影的两侧, 说明线段ab的端点在线段cd的两侧.

同理, 再判断一次cd是否在线段ab两侧即可.

求法线 , 求投影 什么的听起来很复杂的样子, 皆有公式可循:

const nx=b.y - a.y,       ny=a.x - b.x;  const normalLine = {  x: nx, y: ny };  

求点c在法线上的投影位置:

const dist= normalLine.x*c.x + normalLine.y*c.y;  

注意: 这里的"投影位置"是一个标量, 表示的是到法线原点的距离, 而不是投影点的坐标.

当我们把图中 点a投影(distA),点b投影(distB),点c投影(distC) 都求出来之后, 就可以很容易的根据各自的大小判断出相对位置.

distA==distB==distC 时, 两条线段共线
distA==distB!=distC 时, 两条线段平行
distA 和 distB 在distC 同侧时, 两条线段不相交.
distA 和 distB 在distC 异侧时, 两条线段是否相交需要再判断点c点d与线段ab的关系.

这个优化 就优化在这里， 回去做一层检测， 然后再去求焦点， 求焦点用的也是固定公式。 我给出下面实现：

static lineLineIntersect(line1, line2) {    const a = line1.start    const b = line1.end    const c = line2.start    const d = line2.end    const interInfo = []    //线段ab的法线N1    const nx1 = b.y - a.y,      ny1 = a.x - b.x    //线段cd的法线N2    const nx2 = d.y - c.y,      ny2 = c.x - d.x    //两条法线做叉乘, 如果结果为0, 说明线段ab和线段cd平行或共线,不相交    const denominator = nx1 * ny2 - ny1 * nx2    if (denominator == 0) {      return interInfo    }    //在法线N2上的投影    const distC_N2 = nx2 * c.x + ny2 * c.y    const distA_N2 = nx2 * a.x + ny2 * a.y - distC_N2    const distB_N2 = nx2 * b.x + ny2 * b.y - distC_N2    // 点a投影和点b投影在点c投影同侧 (对点在线段上的情况,本例当作不相交处理);    if (distA_N2 * distB_N2 >= 0) {      return interInfo    }    //    //判断点c点d 和线段ab的关系, 原理同上    //    //在法线N1上的投影    const distA_N1 = nx1 * a.x + ny1 * a.y    const distC_N1 = nx1 * c.x + ny1 * c.y - distA_N1    const distD_N1 = nx1 * d.x + ny1 * d.y - distA_N1    if (distC_N1 * distD_N1 >= 0) {      return interInfo    }    //计算交点坐标    const fraction = distA_N2 / denominator    const dx = fraction * ny1,      dy = -fraction * nx1    interInfo.push(new Point2d(a.x + dx, a.y + dy))    return interInfo  }

这个ok 之后，我们去把任意多边形的方法的是否在闭合区域内的方法去实现。

isPointInClosedRegion(event) {    const allSegs = Seg2d.getSegments(this.getDispersed(), true)    // 选取任意一条射线    const start = event.point    const xAxias = new Point2d(1, 0).multiplyScalar(800)    const end = start.clone().add(xAxias)    const anyRaySeg = new Seg2d(start, end)    let total = 0    allSegs.forEach((item) => {      const intersetSegs = Seg2d.lineLineIntersect(item, anyRaySeg)      total += intersetSegs.length    })    // 奇数在内部    if (total % 2 === 1) {      return true    }    return false  }

任意射线，我以鼠标的点，作为起始点， 方向是X轴， 算出终点。 然后得到任意线段。去和所有线段 去求焦点。 统计焦点个数， 来确定是不是在内部。

OK， 这时候我们吧触发事件的条件改写下。

handleEvent = (name) => (event) => {    this.allShapes.forEach((shape) => {      // 获取当前事件的所有监听者      const listerns = shape.listenerMap.get(name)      if (        listerns &&        shape.isPointInClosedRegion(event)      ) {        listerns.forEach((listener) => listener(event))      }    })  }

这样其实就已经实现了，在区域内部实现事件触发了。 看下gif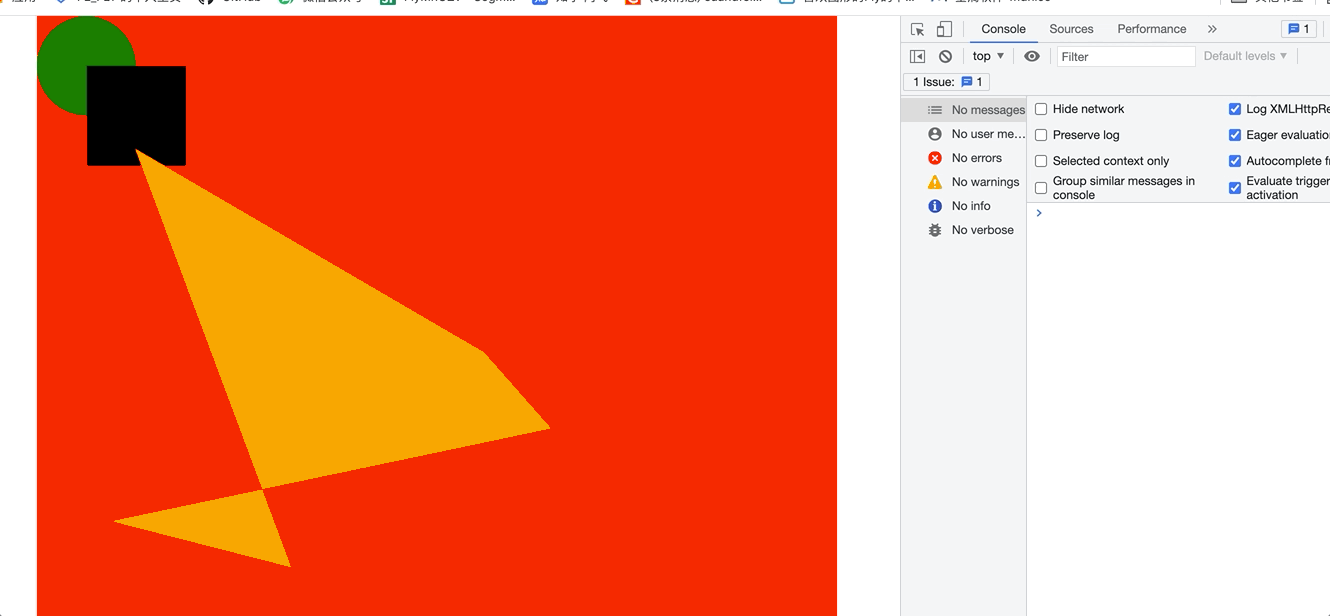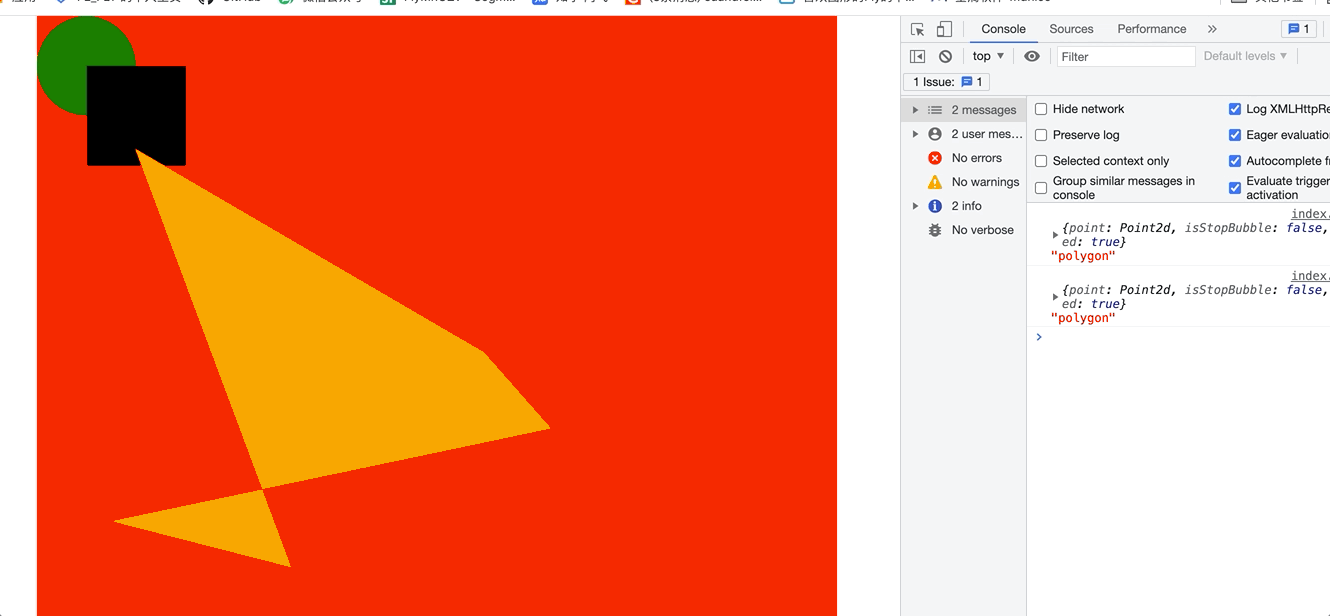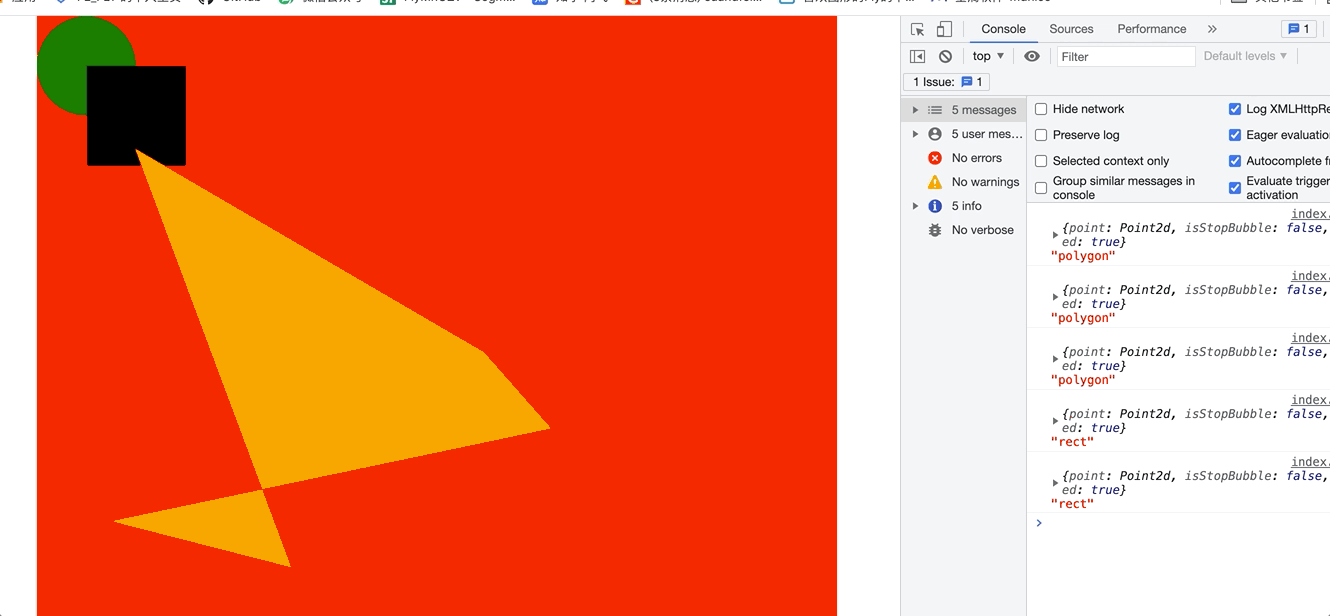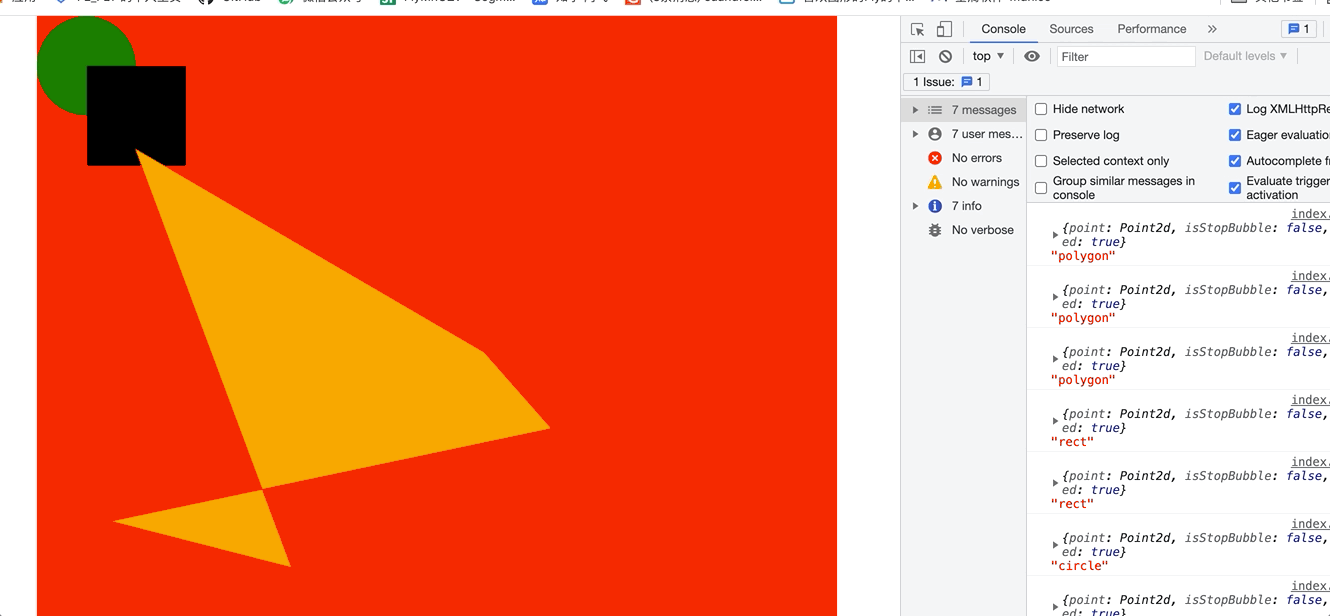

一开始点击的是空白处，然后我分别点了 polygon 和 矩形 和圆形 ，看控制台 你能看到结果。说明我们的算法实现成功了。

阻止事件冒泡

这时候有同学又要问了，我点击两个图形相交的部分，我只想选中内部的， 外面的不想选中。 这是个很正常的需求，首先原生的event 肯定已经满足不了我们了， 解决这个问题就是，分发到这个图形的时候不去触发的所有listeners。不就搞定了。所以我重写了event,其实 也没什么，也就做了两件事

1. 第一件事就是将鼠标的点 转为 point2d
2. 增加一个属性isStopBubble 来阻止冒泡

代码如下：

 getNewEvent(event) {    const point = new Point2d(event.offsetX, event.offsetY)    return {      point,      isStopBubble: false,      ...event,    }  }

我这样的实现的依据是 图形的增加到场景是有序的。这里和大家说下React 事件系统， 由于有Vdom的存在，所以他将事件监听到 document 上， 然后再去按照顺序，去收集所有的lsiteners。 事件的捕获 和冒泡 其实 就是一个 顺序 和倒叙的问题。 他是这么去实现的。 他阻止合成事件冒泡， 就是合成事件有个e.stopPropagation() 。由于我们canvas 没有dom这个概念，所以我们人为封装了一个属性，并且将event传给每个图形 有他们控制 是否阻止。看代码：

handleEvent = (name) => (event) => {    event = this.getNewEvent(event)    this.allShapes.forEach((shape) => {      // 获取当前事件的所有监听者      const listerns = shape.listenerMap.get(name)      if (        listerns &&        shape.isPointInClosedRegion(event)        && !event.isStopBubble      ) {        listerns.forEach((listener) => listener(event))      }    })  }

主要是加了个条件。我们来测试下：

没阻止，我点击公共区域。

阻止冒泡， 代码如下：

circle.on(click, (event) => {  event.isStopBubble = true  console.log(event, 'circle')})rect.on(click, (event) => {  console.log(event, 'rect')})

如图：

总结

本篇文章大概就是简单的实现了canvas 的事件系统了，水平有限，能表达的就这么多。如果有更好的欢迎补充学习和交流，文章有错误的欢迎指正。我是热爱图形的Fly，我们下次再见👋啦。 最后觉得看完对你有帮助的话，点赞👍 再走吧。 知识输出不容易，我会持续持续输出高质量文章的。

资源获得

如果对你有帮助的话，可以关注公众号**【前端图形】**，回复 【事件】 可以获得全部源码。