From 904a08a57a291eb08072ad18fe96373cddb1678c Mon Sep 17 00:00:00 2001
From: "Gaurav S." <44343059+Infonioknight@users.noreply.github.com>
Date: Sun, 6 Oct 2024 17:38:15 +0530
Subject: [PATCH 1/8] Prims Algorithm Tutorial
- Included an overview, the complexities of the algorithm
- Explained one leetcode problem in depth (I couldn't find too many and I wanted to leave some for the suggested problems that were simple and similar)
- Included two suggested problems.
- Highlighted any references used.
---
tutorials/graph-theory/prims-algorithm.md | 130 +++++++++++++++++++++-
1 file changed, 128 insertions(+), 2 deletions(-)
diff --git a/tutorials/graph-theory/prims-algorithm.md b/tutorials/graph-theory/prims-algorithm.md
index 73f31cdcd03..6101cb62413 100644
--- a/tutorials/graph-theory/prims-algorithm.md
+++ b/tutorials/graph-theory/prims-algorithm.md
@@ -1,6 +1,6 @@
---
title: "Prim's Algorithm"
-description: 'Coming Soon!'
+description: "Prim's algorithm finds the Minimum Spanning Tree (MST) of a graph, ensuring all vertices are connected with the smallest possible total edge weight in O(E + V log V) time."
draft: true
keywords:
- leetcode
@@ -9,4 +9,130 @@ keywords:
- algorithm
---
-Coming Soon
\ No newline at end of file
+## Suggested Pre-requisites
+Before moving on to learn the Prims algorithm, it is suggested that you know what a [Minimum Spanning Tree (MST)](../graph-theory/minimum-spanning-tree.md) is.
+
+## Overview
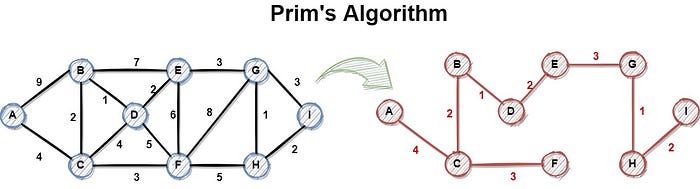
+The Prims algorithm is a [Greedy Algorithm](../basic-topics/greedy.md) used to find a minimum spanning tree (MST) for a connected weighted undirected graph. In simpler terms, it finds a subset of the edges that forms a tree that includes *every* vertex, where the total **weight** of all the **edges** in the tree is **minimized**.
+
+### How does it work?
+- It starts with a single vertex (that can be randomly chosen) and gradually expands the tree by adding the smallest edge that connects a vertex present in the tree to a vertex not yet in the tree.
+- It continues until every vertex is included in the tree.
+- The algorithm uses a priority queue or similar structure to efficiently track the smallest edge that can be added to the tree at each step.
+
+**Note:** Since the starting vertex is chosen at random, it is possible to have different edges included in the MST for the same graph, but the total edge weight of the MST will still have the same minimum value.
+
+### Complexity and Use-Cases
+When implemented using a priority queue (usually a binary heap), the time complexity of Prim’s algorithm is $O(E + V log V)$, where E is the number of edges and V is the number of vertices. This makes Prim's algorithm highly efficient for **dense** graphs, where the number of edges is close to the maximum possible. For sparse graphs (a graph with a relatively small number of edges compared to the maximum number of possible edges), other algorithms like [Kruskal’s](kruskals-algorithm.md) may perform better.
+
+The space complexity of the Prims Algorithm is $O(V + E)$, where V is the number of vertices and E is the number of edges.
+
+Prim's algorithm is widely used in network design, where the goal is to minimize the cost of building a network while connecting all nodes. Examples include laying cables, designing road networks, or creating efficient communication paths. It is also used as a building block in other algorithms for solving more complex problems.
+
+
+
+## Example [1135 - Connecting Cities With Minimum Cost](https://leetcode.com/problems/connecting-cities-with-minimum-cost/description/?envType=problem-list-v2&envId=minimum-spanning-tree)
+**Note:** The above link requires the Leetcode Subscription. To view the problem, use [this](https://leetcode.ca/all/1135.html) alternate link.
+
+### Instructions:
+- There are N cities numbered from 1 to N.
+- You are given connections, where each connections[i] = [city1, city2, cost] represents the cost to connect city1 and city2 together. The connections are all bidirectional.
+- Return the minimum cost so that for every pair of cities, there exists a path of connections (possibly of length 1) that connects those two cities together. The cost is the sum of the connection costs used. If the task is impossible, return -1.
+
+Example:
+**Input:** N = 3, connections = [[1,2,5],[1,3,6],[2,3,1]]
+**Output:** 6
+
+### Approach
+First, we convert the given 'connections' array, into an adjacency list for ease of traversing.
+```python3
+connections = [[1,2,5],[1,3,6],[2,3,1]] # Example
+adjacency_list = {}
+
+for connection in connections:
+ if connection[0] not in adjacency_list:
+ adjacency_list[connection[0]] = []
+ if connection[1] not in adjacency_list:
+ adjacency_list[connection[1]] = []
+ adjacency_list[connection[0]].append((connection[2], connection[1]))
+ adjacency_list[connection[1]].append((connection[2], connection[0]))
+```
+The adjacency list will look like:
+```
+1: [(5, 2), (6, 3)]
+2: [(5, 1), (1, 3)]
+3: [(6, 1), (1, 2)]
+```
+Where each tuple consists of '(cost, destination)'.
+
+Now, to find the minimum cost, we use the below code.
+```python3
+import random
+import heapq
+
+# Number of nodes in the given tree
+N = len(adjacency_list)
+# A list which we will use to implement a priority queue
+connection_queue = []
+# Total minimum cost to traverse all the cities
+solution = 0
+# Taking the assumption that the N nodes in the adjacency list are from 1 to N
+start = random.randint(1, N)
+# To ensure we don't create closed loops
+seen = set([start])
+
+for connection in adjacency_list[start]:
+ heapq.heappush(connection_queue, connection)
+
+while len(seen) < N and connection_queue:
+ cost, current = heapq.heappop(connection_queue)
+ if current in seen:
+ continue
+
+ solution += cost
+ seen.add(current)
+
+ for connection in adjacency_list[current]:
+ if connection[1] not in seen:
+ heapq.heappush(connection_queue, connection)
+
+if len(seen) < N: print(-1)
+else: print(solution)
+```
+
+#### Explanation:
+```python3
+for connection in adjacency_list[start]:
+ heapq.heappush(connection_queue, connection)
+```
+First, we push all the connections of the starting node into the priority queue. On doing so, the nodes with edges of MINIMUM COST come in front.
+
+```python3
+while len(seen) < N and connection_queue:
+ cost, current = heapq.heappop(connection_queue)
+ if current in seen:
+ continue
+
+ solution += cost
+ seen.add(current)
+```
+- Then, we take the first element out of the queue (this is the node we ideally will add to our MST as it will have the minimum cost. We also ensure that the node selected hasn't already been visited.
+- If the node hasn't been visited, we then add the cost to our solution and mark the node as visited.
+
+```python3
+for connection in adjacency_list[current]:
+ if connection[1] not in seen:
+ heapq.heappush(connection_queue, connection)
+
+if len(seen) < N: print(-1)
+else: print(solution)
+```
+- After that, we check the adjacency list for all the nodes connected to the current node (the node visited most recently) and if the connections of this node haven't been visited, they are added to the priority queue.
+- This process goes on until one of two outcomes is achieved.
+ - **Not all** the nodes have been visited, in which case the number of nodes in 'seen' will be less than the total number of nodes. In this case, we do not have a successful output and print **-1**
+ - If all the nodes have been visited, we print the solution.
+
+export const suggestedProblems = [ { "problemName": "1584 - Min Cost to Connect All Points", "difficulty": "Medium", "leetCodeLink": "https://leetcode.com/problems/min-cost-to-connect-all-points/", "solutionLink": "" }, { "problemName": "0787 - Cheapest Flights Within K Stops", "difficulty": "Medium", "leetCodeLink": "https://leetcode.com/problems/cheapest-flights-within-k-stops/", "solutionLink": "" },]
+
+## References:
+1. For the Prim's Algorithm image: https://miro.medium.com/max/700/1*7kpPIPcmXr38Juh0umM6fA.jpeg
From 8545f87c895ba5eaea5efac8c874e763b5cbb7cf Mon Sep 17 00:00:00 2001
From: "Gaurav S." <44343059+Infonioknight@users.noreply.github.com>
Date: Sun, 6 Oct 2024 18:54:52 +0530
Subject: [PATCH 2/8] Update prims-algorithm.md
Incorporated the requested changes.
---
tutorials/graph-theory/prims-algorithm.md | 154 ++++++++++++++--------
1 file changed, 101 insertions(+), 53 deletions(-)
diff --git a/tutorials/graph-theory/prims-algorithm.md b/tutorials/graph-theory/prims-algorithm.md
index 6101cb62413..b95eb460993 100644
--- a/tutorials/graph-theory/prims-algorithm.md
+++ b/tutorials/graph-theory/prims-algorithm.md
@@ -8,6 +8,7 @@ keywords:
- prim
- algorithm
---
+
## Suggested Pre-requisites
Before moving on to learn the Prims algorithm, it is suggested that you know what a [Minimum Spanning Tree (MST)](../graph-theory/minimum-spanning-tree.md) is.
@@ -23,29 +24,38 @@ The Prims algorithm is a [Greedy Algorithm](../basic-topics/greedy.md) used to
**Note:** Since the starting vertex is chosen at random, it is possible to have different edges included in the MST for the same graph, but the total edge weight of the MST will still have the same minimum value.
### Complexity and Use-Cases
-When implemented using a priority queue (usually a binary heap), the time complexity of Prim’s algorithm is $O(E + V log V)$, where E is the number of edges and V is the number of vertices. This makes Prim's algorithm highly efficient for **dense** graphs, where the number of edges is close to the maximum possible. For sparse graphs (a graph with a relatively small number of edges compared to the maximum number of possible edges), other algorithms like [Kruskal’s](kruskals-algorithm.md) may perform better.
+When implemented using a priority queue (usually a binary heap), the time complexity of Prim’s algorithm is $O(E + V log V)$, where $E$ is the number of edges and $V$ is the number of vertices. This makes Prim's algorithm highly efficient for **dense** graphs, where the number of edges is close to the maximum possible. For sparse graphs (a graph with a relatively small number of edges compared to the maximum number of possible edges), other algorithms like [Kruskal’s](kruskals-algorithm.md) may perform better.
-The space complexity of the Prims Algorithm is $O(V + E)$, where V is the number of vertices and E is the number of edges.
+The space complexity of the Prims Algorithm is $O(V + E)$, where $V$ is the number of vertices and $E$ is the number of edges.
Prim's algorithm is widely used in network design, where the goal is to minimize the cost of building a network while connecting all nodes. Examples include laying cables, designing road networks, or creating efficient communication paths. It is also used as a building block in other algorithms for solving more complex problems.

+_Source: https://miro.medium.com/max/700/1*7kpPIPcmXr38Juh0umM6fA.jpeg_
+
## Example [1135 - Connecting Cities With Minimum Cost](https://leetcode.com/problems/connecting-cities-with-minimum-cost/description/?envType=problem-list-v2&envId=minimum-spanning-tree)
**Note:** The above link requires the Leetcode Subscription. To view the problem, use [this](https://leetcode.ca/all/1135.html) alternate link.
### Instructions:
- There are N cities numbered from 1 to N.
-- You are given connections, where each connections[i] = [city1, city2, cost] represents the cost to connect city1 and city2 together. The connections are all bidirectional.
-- Return the minimum cost so that for every pair of cities, there exists a path of connections (possibly of length 1) that connects those two cities together. The cost is the sum of the connection costs used. If the task is impossible, return -1.
+- You are given connections, where each `connections[i] = [city1, city2, cost]` represents the cost to connect `city1` and `city2 ` together. The connections are all bidirectional.
+- Return the minimum cost so that for every pair of cities, there exists a path of connections (possibly of length 1) that connects those two cities together. The cost is the sum of the connection costs used. If the task is impossible, return $-1$.
Example:
-**Input:** N = 3, connections = [[1,2,5],[1,3,6],[2,3,1]]
-**Output:** 6
+
+**Input:** N = `3`, connections = `[[1,2,5],[1,3,6],[2,3,1]]`
+
+**Output:** `6`
### Approach
First, we convert the given 'connections' array, into an adjacency list for ease of traversing.
-```python3
+
+
+
+
+
+```py
connections = [[1,2,5],[1,3,6],[2,3,1]] # Example
adjacency_list = {}
@@ -57,6 +67,8 @@ for connection in connections:
adjacency_list[connection[0]].append((connection[2], connection[1]))
adjacency_list[connection[1]].append((connection[2], connection[0]))
```
+
+
The adjacency list will look like:
```
1: [(5, 2), (6, 3)]
@@ -65,74 +77,110 @@ The adjacency list will look like:
```
Where each tuple consists of '(cost, destination)'.
-Now, to find the minimum cost, we use the below code.
-```python3
-import random
-import heapq
+Now, to find the minimum cost, we use the below approach.
+#### Explanation:
-# Number of nodes in the given tree
-N = len(adjacency_list)
-# A list which we will use to implement a priority queue
-connection_queue = []
-# Total minimum cost to traverse all the cities
-solution = 0
-# Taking the assumption that the N nodes in the adjacency list are from 1 to N
-start = random.randint(1, N)
-# To ensure we don't create closed loops
-seen = set([start])
+
+
+```py
for connection in adjacency_list[start]:
heapq.heappush(connection_queue, connection)
-
-while len(seen) < N and connection_queue:
- cost, current = heapq.heappop(connection_queue)
- if current in seen:
- continue
-
- solution += cost
- seen.add(current)
-
- for connection in adjacency_list[current]:
- if connection[1] not in seen:
- heapq.heappush(connection_queue, connection)
-
-if len(seen) < N: print(-1)
-else: print(solution)
```
+
-#### Explanation:
-```python3
-for connection in adjacency_list[start]:
- heapq.heappush(connection_queue, connection)
-```
First, we push all the connections of the starting node into the priority queue. On doing so, the nodes with edges of MINIMUM COST come in front.
-```python3
-while len(seen) < N and connection_queue:
+
+
+
+```py
+while len(seen) < n and connection_queue:
cost, current = heapq.heappop(connection_queue)
if current in seen:
continue
- solution += cost
+ res += cost
seen.add(current)
```
+
+
- Then, we take the first element out of the queue (this is the node we ideally will add to our MST as it will have the minimum cost. We also ensure that the node selected hasn't already been visited.
- If the node hasn't been visited, we then add the cost to our solution and mark the node as visited.
-```python3
-for connection in adjacency_list[current]:
+
+
+
+```py
+ for connection in adjacency_list[current]:
if connection[1] not in seen:
heapq.heappush(connection_queue, connection)
-if len(seen) < N: print(-1)
-else: print(solution)
+if len(seen) < n: return -1
+else: return res
```
+
+
- After that, we check the adjacency list for all the nodes connected to the current node (the node visited most recently) and if the connections of this node haven't been visited, they are added to the priority queue.
- This process goes on until one of two outcomes is achieved.
- - **Not all** the nodes have been visited, in which case the number of nodes in 'seen' will be less than the total number of nodes. In this case, we do not have a successful output and print **-1**
- - If all the nodes have been visited, we print the solution.
+ - **Not all** the nodes have been visited, in which case the number of nodes in 'seen' will be less than the total number of nodes. In this case, we do not have a successful output and return $-1$
+ - If all the nodes have been visited, we return the solution.
+
+#### Final Code:
-export const suggestedProblems = [ { "problemName": "1584 - Min Cost to Connect All Points", "difficulty": "Medium", "leetCodeLink": "https://leetcode.com/problems/min-cost-to-connect-all-points/", "solutionLink": "" }, { "problemName": "0787 - Cheapest Flights Within K Stops", "difficulty": "Medium", "leetCodeLink": "https://leetcode.com/problems/cheapest-flights-within-k-stops/", "solutionLink": "" },]
+
+
+
+```py
+import random
+import heapq
-## References:
-1. For the Prim's Algorithm image: https://miro.medium.com/max/700/1*7kpPIPcmXr38Juh0umM6fA.jpeg
+def connecting_cities_with_minimum_cost(adjacency_list):
+ # Number of nodes in the given tree
+ n = len(adjacency_list)
+ # A list we will use to implement a priority queue
+ connection_queue = []
+ # Total minimum cost to traverse all the cities
+ res = 0
+ # Taking the assumption that the n nodes in the adjacency list are from 1 to n
+ start = random.randint(1, n)
+ # To ensure we don't create closed loops
+ seen = set([start])
+
+ for connection in adjacency_list[start]:
+ heapq.heappush(connection_queue, connection)
+
+ while len(seen) < n and connection_queue:
+ cost, current = heapq.heappop(connection_queue)
+ if current in seen:
+ continue
+
+ res += cost
+ seen.add(current)
+
+ for connection in adjacency_list[current]:
+ if connection[1] not in seen:
+ heapq.heappush(connection_queue, connection)
+
+ if len(seen) < n: return -1
+ else: return res
+```
+
+
+
+export const suggestedProblems = [
+ {
+ "problemName": "1584 - Min Cost to Connect All Points",
+ "difficulty": "Medium",
+ "leetCodeLink": "https://leetcode.com/problems/min-cost-to-connect-all-points/",
+ "solutionLink": ""
+ },
+ {
+ "problemName": "0787 - Cheapest Flights Within K Stops",
+ "difficulty": "Medium",
+ "leetCodeLink": "https://leetcode.com/problems/cheapest-flights-within-k-stops/",
+ "solutionLink": ""
+ },
+]
+
+
From 590a2a35859ebc8b887d6a4b5554fa75e375c2a8 Mon Sep 17 00:00:00 2001
From: "Gaurav S." <44343059+Infonioknight@users.noreply.github.com>
Date: Sun, 6 Oct 2024 23:01:13 +0530
Subject: [PATCH 3/8] Update prims-algorithm.md
- Added a second example problem for the same.
---
tutorials/graph-theory/prims-algorithm.md | 194 ++++++++++++++++++++--
1 file changed, 181 insertions(+), 13 deletions(-)
diff --git a/tutorials/graph-theory/prims-algorithm.md b/tutorials/graph-theory/prims-algorithm.md
index b95eb460993..9cda74380a2 100644
--- a/tutorials/graph-theory/prims-algorithm.md
+++ b/tutorials/graph-theory/prims-algorithm.md
@@ -34,7 +34,7 @@ Prim's algorithm is widely used in network design, where the goal is to minimize
_Source: https://miro.medium.com/max/700/1*7kpPIPcmXr38Juh0umM6fA.jpeg_
-## Example [1135 - Connecting Cities With Minimum Cost](https://leetcode.com/problems/connecting-cities-with-minimum-cost/description/?envType=problem-list-v2&envId=minimum-spanning-tree)
+## Example 1: [1135 - Connecting Cities With Minimum Cost](https://leetcode.com/problems/connecting-cities-with-minimum-cost/description/?envType=problem-list-v2&envId=minimum-spanning-tree)
**Note:** The above link requires the Leetcode Subscription. To view the problem, use [this](https://leetcode.ca/all/1135.html) alternate link.
### Instructions:
@@ -42,7 +42,7 @@ _Source: https://miro.medium.com/max/700/1*7kpPIPcmXr38Juh0umM6fA.jpeg_
- You are given connections, where each `connections[i] = [city1, city2, cost]` represents the cost to connect `city1` and `city2 ` together. The connections are all bidirectional.
- Return the minimum cost so that for every pair of cities, there exists a path of connections (possibly of length 1) that connects those two cities together. The cost is the sum of the connection costs used. If the task is impossible, return $-1$.
-Example:
+#### Example:
**Input:** N = `3`, connections = `[[1,2,5],[1,3,6],[2,3,1]]`
@@ -78,7 +78,7 @@ The adjacency list will look like:
Where each tuple consists of '(cost, destination)'.
Now, to find the minimum cost, we use the below approach.
-#### Explanation:
+### Explanation:
@@ -135,18 +135,131 @@ else: return res
import random
import heapq
-def connecting_cities_with_minimum_cost(adjacency_list):
+class Solution:
+ def connecting_cities_with_minimum_cost(adjacency_list):
+ # Number of nodes in the given tree
+ n = len(adjacency_list)
+ # A list we will use to implement a priority queue
+ connection_queue = []
+ # Total minimum cost to traverse all the cities
+ res = 0
+ # Taking the assumption that the n nodes in the adjacency list are from 1 to n
+ start = random.randint(1, n)
+ # To ensure we don't create closed loops
+ seen = set([start])
+
+ for connection in adjacency_list[start]:
+ heapq.heappush(connection_queue, connection)
+
+ while len(seen) < n and connection_queue:
+ cost, current = heapq.heappop(connection_queue)
+ if current in seen:
+ continue
+
+ res += cost
+ seen.add(current)
+
+ for connection in adjacency_list[current]:
+ if connection[1] not in seen:
+ heapq.heappush(connection_queue, connection)
+
+ if len(seen) < n: return -1
+ return res
+
+
+ def minimumCost(self, n: int, connections: List[List[int]]) -> int:
+ adjacency_list = {}
+
+ for connection in connections:
+ if connection[0] not in adjacency_list:
+ adjacency_list[connection[0]] = []
+ if connection[1] not in adjacency_list:
+ adjacency_list[connection[1]] = []
+ adjacency_list[connection[0]].append((connection[2], connection[1]))
+ adjacency_list[connection[1]].append((connection[2], connection[0]))
+
+ return connecting_cities_with_minimum_cost(adjacency_list)
+```
+
+
+
+## Example 2: [1584 - Min Cost to Connect All Points](https://leetcode.com/problems/min-cost-to-connect-all-points)
+### Instructions:
+You are given an array `points` representing integer coordinates of some points on a 2D-plane, where `points[i]` = `[xi, yi]`.
+The cost of connecting two points `[xi, yi]` and `[xj, yj]` is the **Manhattan distance** between them: `|xi - xj|` + `|yi - yj|`, where `|val|` denotes the absolute value of `val`.
+
+Return the minimum cost to make all points connected. All points are connected if there is exactly one simple path between any two points.
+
+#### Example:
+
+**Input:** points = `[[0,0],[2,2],[3,10],[5,2],[7,0]]`
+
+**Output:** `20`
+
+### Approach
+- This problem is also, extremely similar to the previous one. Only difference being the way the input is provided here (as a list of points, where you calculate the weight of the edges)
+- The approach I would suggest, would be to assume this as a **Complete Tree** (Every node is connected to every other node). So the way to convert the given points, into an adjacency list would be as below.
+
+
+
+
+
+
+```py
+points = [[0,0],[2,2],[3,10],[5,2],[7,0]]
+
+adjacency_list = {}
+for i in range(len(points)):
+ current = tuple(points[i])
+ for j in range(i+1, len(points)):
+ destination = tuple(points[j])
+ if current not in adjacency_list:
+ adjacency_list[current] = []
+ if destination not in adjacency_list:
+ adjacency_list[destination] = []
+
+ # The formula in the second item of the append, is to calculate the Manhattan Distance between two points (the edge weight)
+ adjacency_list[current].append([abs(destination[0] - current[0]) + abs(destination[1] - current[1]), destination])
+ adjacency_list[destination].append([abs(destination[0] - current[0]) + abs(destination[1] - current[1]), current])
+```
+
+
+The adjacency list, will look something like this:
+```
+(0, 0): [[4, (2, 2)], [13, (3, 10)], [7, (5, 2)], [7, (7, 0)]]
+(2, 2): [[4, (0, 0)], [9, (3, 10)], [3, (5, 2)], [7, (7, 0)]]
+(3, 10): [[13, (0, 0)], [9, (2, 2)], [10, (5, 2)], [14, (7, 0)]]
+(5, 2): [[7, (0, 0)], [3, (2, 2)], [10, (3, 10)], [4, (7, 0)]]
+(7, 0): [[7, (0, 0)], [7, (2, 2)], [14, (3, 10)], [4, (5, 2)]]
+```
+
+The rest of the code follows an almost identical pattern as the previous one. The below being probably the only changes regarding to how the entire traversal is started.
+
+
+
+
+```py
+# Here, our helper function contains one additional argument - the initial point (as here we don't need to randomly start)
+def min_cost_points(adjacency_list, initial):
# Number of nodes in the given tree
n = len(adjacency_list)
# A list we will use to implement a priority queue
connection_queue = []
- # Total minimum cost to traverse all the cities
+ # Total minimum cost to connect all points
res = 0
- # Taking the assumption that the n nodes in the adjacency list are from 1 to n
- start = random.randint(1, n)
+ start = tuple(initial)
# To ensure we don't create closed loops
seen = set([start])
+```
+
+
+The below is the implementation of the main function. It is identical to the previous example in every way except for the final output (as in this question, we are guaranteed a solution)
+
+
+
+
+```py
for connection in adjacency_list[start]:
heapq.heappush(connection_queue, connection)
@@ -162,24 +275,79 @@ def connecting_cities_with_minimum_cost(adjacency_list):
if connection[1] not in seen:
heapq.heappush(connection_queue, connection)
- if len(seen) < n: return -1
- else: return res
+ return res
+```
+
+
+#### Final Code:
+
+
+
+
+```py
+import heapq
+
+class Solution:
+ def min_cost_points(adjacency_list, initial):
+ # Number of nodes in the given tree
+ n = len(adjacency_list)
+ # A list we will use to implement a priority queue
+ connection_queue = []
+ # Total minimum cost to connect all points
+ res = 0
+ # Taking the assumption that the n nodes in the adjacency list are from 1 to n
+ start = tuple(initial)
+ # To ensure we don't create closed loops
+ seen = set([start])
+
+ for connection in adjacency_list[start]:
+ heapq.heappush(connection_queue, connection)
+
+ while len(seen) < n and connection_queue:
+ cost, current = heapq.heappop(connection_queue)
+ if current in seen:
+ continue
+
+ res += cost
+ seen.add(current)
+
+ for connection in adjacency_list[current]:
+ if connection[1] not in seen:
+ heapq.heappush(connection_queue, connection)
+
+ return res
+
+ def minCostConnectPoints(self, points: List[List[int]]) -> int:
+ adjacency_list = {}
+ for i in range(len(points)):
+ current = tuple(points[i])
+ for j in range(i+1, len(points)):
+ destination = tuple(points[j])
+ if current not in adjacency_list:
+ adjacency_list[current] = []
+ if destination not in adjacency_list:
+ adjacency_list[destination] = []
+
+ adjacency_list[current].append([abs(destination[0] - current[0]) + abs(destination[1] - current[1]), destination])
+ adjacency_list[destination].append([abs(destination[0] - current[0]) + abs(destination[1] - current[1]), current])
+
+ return min_cost_points(adjacency_list, points[0])
```
export const suggestedProblems = [
{
- "problemName": "1584 - Min Cost to Connect All Points",
- "difficulty": "Medium",
- "leetCodeLink": "https://leetcode.com/problems/min-cost-to-connect-all-points/",
+ "problemName": "1489. Find Critical and Pseudo-Critical Edges in Minimum Spanning Tree",
+ "difficulty": "Hard",
+ "leetCodeLink": "https://leetcode.com/problems/find-critical-and-pseudo-critical-edges-in-minimum-spanning-tree/",
"solutionLink": ""
},
{
"problemName": "0787 - Cheapest Flights Within K Stops",
"difficulty": "Medium",
"leetCodeLink": "https://leetcode.com/problems/cheapest-flights-within-k-stops/",
- "solutionLink": ""
+ "solutionLink": "../../solutions/0700-0799/0787-cheapest-flights-within-k-stops-medium.md"
},
]
From 68a45b2ed2ae5f7443a63d0d07022aa1fc0a2a02 Mon Sep 17 00:00:00 2001
From: "Gaurav S." <44343059+Infonioknight@users.noreply.github.com>
Date: Mon, 7 Oct 2024 03:22:29 +0530
Subject: [PATCH 4/8] Update prims-algorithm.md
Made a few modifications to the code, indentation to make it copy-pastable in leetcode
---
tutorials/graph-theory/prims-algorithm.md | 88 ++++++++++++-----------
1 file changed, 45 insertions(+), 43 deletions(-)
diff --git a/tutorials/graph-theory/prims-algorithm.md b/tutorials/graph-theory/prims-algorithm.md
index 9cda74380a2..649a1dde7ae 100644
--- a/tutorials/graph-theory/prims-algorithm.md
+++ b/tutorials/graph-theory/prims-algorithm.md
@@ -136,7 +136,7 @@ import random
import heapq
class Solution:
- def connecting_cities_with_minimum_cost(adjacency_list):
+ def connecting_cities_with_minimum_cost(self, adjacency_list):
# Number of nodes in the given tree
n = len(adjacency_list)
# A list we will use to implement a priority queue
@@ -178,7 +178,7 @@ class Solution:
adjacency_list[connection[0]].append((connection[2], connection[1]))
adjacency_list[connection[1]].append((connection[2], connection[0]))
- return connecting_cities_with_minimum_cost(adjacency_list)
+ return self.connecting_cities_with_minimum_cost(adjacency_list)
```
@@ -288,50 +288,52 @@ The below is the implementation of the main function. It is identical to the pre
import heapq
class Solution:
- def min_cost_points(adjacency_list, initial):
- # Number of nodes in the given tree
- n = len(adjacency_list)
- # A list we will use to implement a priority queue
- connection_queue = []
- # Total minimum cost to connect all points
- res = 0
- # Taking the assumption that the n nodes in the adjacency list are from 1 to n
- start = tuple(initial)
- # To ensure we don't create closed loops
- seen = set([start])
-
- for connection in adjacency_list[start]:
- heapq.heappush(connection_queue, connection)
-
- while len(seen) < n and connection_queue:
- cost, current = heapq.heappop(connection_queue)
- if current in seen:
- continue
-
- res += cost
- seen.add(current)
-
- for connection in adjacency_list[current]:
- if connection[1] not in seen:
- heapq.heappush(connection_queue, connection)
-
- return res
+ def min_cost_points(self, adjacency_list, initial):
+ # Number of nodes in the given tree
+ n = len(adjacency_list)
+ # A list we will use to implement a priority queue
+ connection_queue = []
+ # Total minimum cost to connect all points
+ res = 0
+ # Taking the assumption that the n nodes in the adjacency list are from 1 to n
+ start = tuple(initial)
+ # To ensure we don't create closed loops
+ seen = set([start])
+
+ for connection in adjacency_list[start]:
+ heapq.heappush(connection_queue, connection)
+
+ while len(seen) < n and connection_queue:
+ cost, current = heapq.heappop(connection_queue)
+ if current in seen:
+ continue
+
+ res += cost
+ seen.add(current)
+
+ for connection in adjacency_list[current]:
+ if connection[1] not in seen:
+ heapq.heappush(connection_queue, connection)
+
+ return res
- def minCostConnectPoints(self, points: List[List[int]]) -> int:
- adjacency_list = {}
- for i in range(len(points)):
- current = tuple(points[i])
- for j in range(i+1, len(points)):
- destination = tuple(points[j])
- if current not in adjacency_list:
- adjacency_list[current] = []
- if destination not in adjacency_list:
- adjacency_list[destination] = []
+ def minCostConnectPoints(self, points: List[List[int]]) -> int:
+ adjacency_list = {}
+ for i in range(len(points)):
+ current = tuple(points[i])
+ for j in range(i+1, len(points)):
+ destination = tuple(points[j])
+ if current not in adjacency_list:
+ adjacency_list[current] = []
+ if destination not in adjacency_list:
+ adjacency_list[destination] = []
- adjacency_list[current].append([abs(destination[0] - current[0]) + abs(destination[1] - current[1]), destination])
- adjacency_list[destination].append([abs(destination[0] - current[0]) + abs(destination[1] - current[1]), current])
+ adjacency_list[current].append([abs(destination[0] - current[0]) + abs(destination[1] - current[1]), destination])
+ adjacency_list[destination].append([abs(destination[0] - current[0]) + abs(destination[1] - current[1]), current])
- return min_cost_points(adjacency_list, points[0])
+ if len(points) < 2:
+ return 0
+ return self.min_cost_points(adjacency_list, points[0])
```
From a09a98c015175c29c43e3893f18158f234a31247 Mon Sep 17 00:00:00 2001
From: "Gaurav S." <44343059+Infonioknight@users.noreply.github.com>
Date: Sun, 27 Oct 2024 22:19:49 +0530
Subject: [PATCH 5/8] Update prims-algorithm.md
Made necessary changes to run locally
---
tutorials/graph-theory/prims-algorithm.md | 32 ++++++++++++++++-------
1 file changed, 23 insertions(+), 9 deletions(-)
diff --git a/tutorials/graph-theory/prims-algorithm.md b/tutorials/graph-theory/prims-algorithm.md
index 649a1dde7ae..f65e0bdddcf 100644
--- a/tutorials/graph-theory/prims-algorithm.md
+++ b/tutorials/graph-theory/prims-algorithm.md
@@ -52,7 +52,7 @@ _Source: https://miro.medium.com/max/700/1*7kpPIPcmXr38Juh0umM6fA.jpeg_
First, we convert the given 'connections' array, into an adjacency list for ease of traversing.
-
+
```py
@@ -68,6 +68,7 @@ for connection in connections:
adjacency_list[connection[1]].append((connection[2], connection[0]))
```
+
The adjacency list will look like:
```
@@ -80,7 +81,8 @@ Where each tuple consists of '(cost, destination)'.
Now, to find the minimum cost, we use the below approach.
### Explanation:
-
+
+
```py
@@ -88,10 +90,12 @@ for connection in adjacency_list[start]:
heapq.heappush(connection_queue, connection)
```
+
First, we push all the connections of the starting node into the priority queue. On doing so, the nodes with edges of MINIMUM COST come in front.
-
+
+
```py
@@ -104,11 +108,13 @@ while len(seen) < n and connection_queue:
seen.add(current)
```
+
- Then, we take the first element out of the queue (this is the node we ideally will add to our MST as it will have the minimum cost. We also ensure that the node selected hasn't already been visited.
- If the node hasn't been visited, we then add the cost to our solution and mark the node as visited.
-
+
+
```py
@@ -120,6 +126,7 @@ if len(seen) < n: return -1
else: return res
```
+
- After that, we check the adjacency list for all the nodes connected to the current node (the node visited most recently) and if the connections of this node haven't been visited, they are added to the priority queue.
- This process goes on until one of two outcomes is achieved.
@@ -128,7 +135,8 @@ else: return res
#### Final Code:
-
+
+
```py
@@ -202,7 +210,7 @@ Return the minimum cost to make all points connected. All points are connected i
-
+
```py
@@ -223,6 +231,7 @@ for i in range(len(points)):
adjacency_list[destination].append([abs(destination[0] - current[0]) + abs(destination[1] - current[1]), current])
```
+
The adjacency list, will look something like this:
```
@@ -235,7 +244,8 @@ The adjacency list, will look something like this:
The rest of the code follows an almost identical pattern as the previous one. The below being probably the only changes regarding to how the entire traversal is started.
-
+
+
```py
@@ -253,10 +263,12 @@ def min_cost_points(adjacency_list, initial):
```
+
The below is the implementation of the main function. It is identical to the previous example in every way except for the final output (as in this question, we are guaranteed a solution)
-
+
+
```py
@@ -278,10 +290,12 @@ The below is the implementation of the main function. It is identical to the pre
return res
```
+
#### Final Code:
-
+
+
```py
From 2d9bca1ea548442d24f8de2d58850d67d693721f Mon Sep 17 00:00:00 2001
From: "Gaurav S." <44343059+Infonioknight@users.noreply.github.com>
Date: Thu, 31 Oct 2024 02:02:47 +0530
Subject: [PATCH 6/8] Update prims-algorithm.md
- Changed all backtick highlighting to LaTeX
- Modified the introduction to the problems (made it an explanation instead of just listing input and output)
- Changed value for TabItems to 'py'
---
tutorials/graph-theory/prims-algorithm.md | 58 +++++++++++++----------
1 file changed, 33 insertions(+), 25 deletions(-)
diff --git a/tutorials/graph-theory/prims-algorithm.md b/tutorials/graph-theory/prims-algorithm.md
index f65e0bdddcf..1d346da17f8 100644
--- a/tutorials/graph-theory/prims-algorithm.md
+++ b/tutorials/graph-theory/prims-algorithm.md
@@ -37,22 +37,35 @@ _Source: https://miro.medium.com/max/700/1*7kpPIPcmXr38Juh0umM6fA.jpeg_
## Example 1: [1135 - Connecting Cities With Minimum Cost](https://leetcode.com/problems/connecting-cities-with-minimum-cost/description/?envType=problem-list-v2&envId=minimum-spanning-tree)
**Note:** The above link requires the Leetcode Subscription. To view the problem, use [this](https://leetcode.ca/all/1135.html) alternate link.
-### Instructions:
-- There are N cities numbered from 1 to N.
-- You are given connections, where each `connections[i] = [city1, city2, cost]` represents the cost to connect `city1` and `city2 ` together. The connections are all bidirectional.
-- Return the minimum cost so that for every pair of cities, there exists a path of connections (possibly of length 1) that connects those two cities together. The cost is the sum of the connection costs used. If the task is impossible, return $-1$.
+### Example:
+**Input:** $N = 3$, $connections = [[1,2,5],[1,3,6],[2,3,1]]$
+
+First, for clarity we make a note of the connections in a way that's easy to understand.
+
+- $city 1$ and $city 2$ are connected by a path of cost $5$
+- $city 1$ and $city 3$ are connected by a path of cost $6$
+- $city 2$ and $city 3$ are connected by a path of cost $1$
+
+Our goal is to find the minimum so that for every pair of cities, there exists a path of connections that connects these two cities together. If that is possible, we return the $cost$. If it's impossible, we return $-1$
-#### Example:
+Assuming we start at $city 1$, we first pick the smallest connection from here - Namely the one to $city 2$ with a cost of 5
-**Input:** N = `3`, connections = `[[1,2,5],[1,3,6],[2,3,1]]`
+Current total cost = $0 + 5 = 5$
-**Output:** `6`
+Now we have two remaining connections to consider from our connected cities:
+ - Connect $city 2$ to $city 3$ (cost $1$)
+ - Connect $city 1$ to $city 3$ (cost $6$)
+
+Clearly the **cheapest** one, is the one with cost $1$.
+So, the total cost is $5 + 1 = 6$
+
+Now all the cities have been connected. So we return our **solution** $6$.
### Approach
First, we convert the given 'connections' array, into an adjacency list for ease of traversing.
-
+
```py
@@ -82,7 +95,7 @@ Now, to find the minimum cost, we use the below approach.
### Explanation:
-
+
```py
@@ -95,7 +108,7 @@ for connection in adjacency_list[start]:
First, we push all the connections of the starting node into the priority queue. On doing so, the nodes with edges of MINIMUM COST come in front.
-
+
```py
@@ -110,11 +123,11 @@ while len(seen) < n and connection_queue:
-- Then, we take the first element out of the queue (this is the node we ideally will add to our MST as it will have the minimum cost. We also ensure that the node selected hasn't already been visited.
+- Then, we take the first element out of the queue (this is the node we ideally will add to our MST as it will have the minimum cost). We also ensure that the node selected hasn't already been visited.
- If the node hasn't been visited, we then add the cost to our solution and mark the node as visited.
-
+
```py
@@ -136,7 +149,7 @@ else: return res
#### Final Code:
-
+
```py
@@ -193,16 +206,11 @@ class Solution:
## Example 2: [1584 - Min Cost to Connect All Points](https://leetcode.com/problems/min-cost-to-connect-all-points)
### Instructions:
-You are given an array `points` representing integer coordinates of some points on a 2D-plane, where `points[i]` = `[xi, yi]`.
-The cost of connecting two points `[xi, yi]` and `[xj, yj]` is the **Manhattan distance** between them: `|xi - xj|` + `|yi - yj|`, where `|val|` denotes the absolute value of `val`.
+You are given an array $points$ representing integer coordinates of some points on a 2D-plane, where $points[i]$ = $[xi, yi]$.
+The cost of connecting two points $[xi, yi]$ and $[xj, yj]$ is the **Manhattan distance** between them: $|xi - xj|$ + $|yi - yj|$, where $|val|$ denotes the absolute value of $val$.
Return the minimum cost to make all points connected. All points are connected if there is exactly one simple path between any two points.
-#### Example:
-
-**Input:** points = `[[0,0],[2,2],[3,10],[5,2],[7,0]]`
-
-**Output:** `20`
### Approach
- This problem is also, extremely similar to the previous one. Only difference being the way the input is provided here (as a list of points, where you calculate the weight of the edges)
@@ -210,7 +218,7 @@ Return the minimum cost to make all points connected. All points are connected i
-
+
```py
@@ -245,7 +253,7 @@ The adjacency list, will look something like this:
The rest of the code follows an almost identical pattern as the previous one. The below being probably the only changes regarding to how the entire traversal is started.
-
+
```py
@@ -268,7 +276,7 @@ def min_cost_points(adjacency_list, initial):
The below is the implementation of the main function. It is identical to the previous example in every way except for the final output (as in this question, we are guaranteed a solution)
-
+
```py
@@ -295,7 +303,7 @@ The below is the implementation of the main function. It is identical to the pre
#### Final Code:
-
+
```py
@@ -363,7 +371,7 @@ export const suggestedProblems = [
"problemName": "0787 - Cheapest Flights Within K Stops",
"difficulty": "Medium",
"leetCodeLink": "https://leetcode.com/problems/cheapest-flights-within-k-stops/",
- "solutionLink": "../../solutions/0700-0799/0787-cheapest-flights-within-k-stops-medium.md"
+ "solutionLink": "../../solutions/0700-0799/cheapest-flights-within-k-stops-medium"
},
]
From 88e6f9395a7be2ff31880d027ef9eb71e08ad20b Mon Sep 17 00:00:00 2001
From: "Gaurav S." <44343059+Infonioknight@users.noreply.github.com>
Date: Sat, 11 Jan 2025 02:22:20 +0530
Subject: [PATCH 7/8] Update prims-algorithm.md
---
tutorials/graph-theory/prims-algorithm.md | 12 ++++++------
1 file changed, 6 insertions(+), 6 deletions(-)
diff --git a/tutorials/graph-theory/prims-algorithm.md b/tutorials/graph-theory/prims-algorithm.md
index 1d346da17f8..8ba9abd35fa 100644
--- a/tutorials/graph-theory/prims-algorithm.md
+++ b/tutorials/graph-theory/prims-algorithm.md
@@ -37,7 +37,7 @@ _Source: https://miro.medium.com/max/700/1*7kpPIPcmXr38Juh0umM6fA.jpeg_
## Example 1: [1135 - Connecting Cities With Minimum Cost](https://leetcode.com/problems/connecting-cities-with-minimum-cost/description/?envType=problem-list-v2&envId=minimum-spanning-tree)
**Note:** The above link requires the Leetcode Subscription. To view the problem, use [this](https://leetcode.ca/all/1135.html) alternate link.
-### Example:
+### Example
**Input:** $N = 3$, $connections = [[1,2,5],[1,3,6],[2,3,1]]$
First, for clarity we make a note of the connections in a way that's easy to understand.
@@ -56,7 +56,7 @@ Now we have two remaining connections to consider from our connected cities:
- Connect $city 2$ to $city 3$ (cost $1$)
- Connect $city 1$ to $city 3$ (cost $6$)
-Clearly the **cheapest** one, is the one with cost $1$.
+Clearly the **cheapest** one is the one with cost $1$.
So, the total cost is $5 + 1 = 6$
Now all the cities have been connected. So we return our **solution** $6$.
@@ -92,7 +92,7 @@ The adjacency list will look like:
Where each tuple consists of '(cost, destination)'.
Now, to find the minimum cost, we use the below approach.
-### Explanation:
+### Explanation
@@ -146,7 +146,7 @@ else: return res
- **Not all** the nodes have been visited, in which case the number of nodes in 'seen' will be less than the total number of nodes. In this case, we do not have a successful output and return $-1$
- If all the nodes have been visited, we return the solution.
-#### Final Code:
+#### Final Code
@@ -205,7 +205,7 @@ class Solution:
## Example 2: [1584 - Min Cost to Connect All Points](https://leetcode.com/problems/min-cost-to-connect-all-points)
-### Instructions:
+### Instructions
You are given an array $points$ representing integer coordinates of some points on a 2D-plane, where $points[i]$ = $[xi, yi]$.
The cost of connecting two points $[xi, yi]$ and $[xj, yj]$ is the **Manhattan distance** between them: $|xi - xj|$ + $|yi - yj|$, where $|val|$ denotes the absolute value of $val$.
@@ -300,7 +300,7 @@ The below is the implementation of the main function. It is identical to the pre
-#### Final Code:
+#### Final Code
From 44cc32c6765826bba62a31be8b8b4268ca37278a Mon Sep 17 00:00:00 2001
From: "Gaurav S." <44343059+Infonioknight@users.noreply.github.com>
Date: Sat, 11 Jan 2025 03:36:34 +0530
Subject: [PATCH 8/8] Update prims-algorithm.md
---
tutorials/graph-theory/prims-algorithm.md | 274 +++++++++++-----------
1 file changed, 139 insertions(+), 135 deletions(-)
diff --git a/tutorials/graph-theory/prims-algorithm.md b/tutorials/graph-theory/prims-algorithm.md
index 8ba9abd35fa..e7e846f55af 100644
--- a/tutorials/graph-theory/prims-algorithm.md
+++ b/tutorials/graph-theory/prims-algorithm.md
@@ -24,15 +24,16 @@ The Prims algorithm is a [Greedy Algorithm](../basic-topics/greedy.md) used to
**Note:** Since the starting vertex is chosen at random, it is possible to have different edges included in the MST for the same graph, but the total edge weight of the MST will still have the same minimum value.
### Complexity and Use-Cases
-When implemented using a priority queue (usually a binary heap), the time complexity of Prim’s algorithm is $O(E + V log V)$, where $E$ is the number of edges and $V$ is the number of vertices. This makes Prim's algorithm highly efficient for **dense** graphs, where the number of edges is close to the maximum possible. For sparse graphs (a graph with a relatively small number of edges compared to the maximum number of possible edges), other algorithms like [Kruskal’s](kruskals-algorithm.md) may perform better.
+- When implemented using a priority queue (usually a binary heap), the time complexity of Prim’s algorithm is $O((E + V)log V)$ (when implemented using a binary heap), where $E$ is the number of edges and $V$ is the number of vertices.
+- To calculate the time complexity, we know that each extraction operation from a priority queue takes $O(log V)$ time. The algorithm extracts a vertex from this queue a total of $V$ times (traverse the entire graph), and for each edge, the algorithm will have to update the priority of an adjacent vertex. This takes place a total of $E$ times. Combining these two (extraction + updation), processes on the queue take place a total of $(E + V)$ times.
+- This brings us to the final time complexity of $O((E + V)log V)$. This makes Prim's algorithm highly efficient for **dense** graphs, where the number of edges is close to the maximum possible. For sparse graphs (a graph with a relatively small number of edges compared to the maximum number of possible edges), other algorithms like [Kruskal’s](kruskals-algorithm.md) may perform better. This is because of the presence of $O(ElogV)$ term in the time complexity, which doesn't increase the computation time of a priority queue operation $O(log V)$. This is unlike that of Kruskal's where the edges are sorted, which takes $O(Elog E)$ time.
The space complexity of the Prims Algorithm is $O(V + E)$, where $V$ is the number of vertices and $E$ is the number of edges.
Prim's algorithm is widely used in network design, where the goal is to minimize the cost of building a network while connecting all nodes. Examples include laying cables, designing road networks, or creating efficient communication paths. It is also used as a building block in other algorithms for solving more complex problems.
-
-
-_Source: https://miro.medium.com/max/700/1*7kpPIPcmXr38Juh0umM6fA.jpeg_
+
+_Source: https://plainenglish.io/blog/an-introduction-to-prims-algorithm-in-python-8c764df5936f_
## Example 1: [1135 - Connecting Cities With Minimum Cost](https://leetcode.com/problems/connecting-cities-with-minimum-cost/description/?envType=problem-list-v2&envId=minimum-spanning-tree)
**Note:** The above link requires the Leetcode Subscription. To view the problem, use [this](https://leetcode.ca/all/1135.html) alternate link.
@@ -73,12 +74,12 @@ connections = [[1,2,5],[1,3,6],[2,3,1]] # Example
adjacency_list = {}
for connection in connections:
- if connection[0] not in adjacency_list:
- adjacency_list[connection[0]] = []
- if connection[1] not in adjacency_list:
- adjacency_list[connection[1]] = []
- adjacency_list[connection[0]].append((connection[2], connection[1]))
- adjacency_list[connection[1]].append((connection[2], connection[0]))
+ if connection[0] not in adjacency_list:
+ adjacency_list[connection[0]] = []
+ if connection[1] not in adjacency_list:
+ adjacency_list[connection[1]] = []
+ adjacency_list[connection[0]].append((connection[2], connection[1]))
+ adjacency_list[connection[1]].append((connection[2], connection[0]))
```
@@ -89,7 +90,7 @@ The adjacency list will look like:
2: [(5, 1), (1, 3)]
3: [(6, 1), (1, 2)]
```
-Where each tuple consists of '(cost, destination)'.
+Where each tuple consists of $(cost, destination)$.
Now, to find the minimum cost, we use the below approach.
### Explanation
@@ -100,7 +101,7 @@ Now, to find the minimum cost, we use the below approach.
```py
for connection in adjacency_list[start]:
- heapq.heappush(connection_queue, connection)
+ heapq.heappush(connection_queue, connection)
```
@@ -113,12 +114,12 @@ First, we push all the connections of the starting node into the priority queue.
```py
while len(seen) < n and connection_queue:
- cost, current = heapq.heappop(connection_queue)
- if current in seen:
- continue
+ cost, current = heapq.heappop(connection_queue)
+ if current in seen:
+ continue
- res += cost
- seen.add(current)
+ res += cost
+ seen.add(current)
```
@@ -132,8 +133,8 @@ while len(seen) < n and connection_queue:
```py
for connection in adjacency_list[current]:
- if connection[1] not in seen:
- heapq.heappush(connection_queue, connection)
+ if connection[1] not in seen:
+ heapq.heappush(connection_queue, connection)
if len(seen) < n: return -1
else: return res
@@ -158,56 +159,56 @@ import heapq
class Solution:
def connecting_cities_with_minimum_cost(self, adjacency_list):
- # Number of nodes in the given tree
- n = len(adjacency_list)
- # A list we will use to implement a priority queue
- connection_queue = []
- # Total minimum cost to traverse all the cities
- res = 0
- # Taking the assumption that the n nodes in the adjacency list are from 1 to n
- start = random.randint(1, n)
- # To ensure we don't create closed loops
- seen = set([start])
-
- for connection in adjacency_list[start]:
+ # Number of nodes in the given tree
+ n = len(adjacency_list)
+ # A list we will use to implement a priority queue
+ connection_queue = []
+ # Total minimum cost to traverse all the cities
+ res = 0
+ # Taking the assumption that the n nodes in the adjacency list are from 1 to n
+ start = random.randint(1, n)
+ # To ensure we don't create closed loops
+ seen = set([start])
+
+ for connection in adjacency_list[start]:
+ heapq.heappush(connection_queue, connection)
+
+ while len(seen) < n and connection_queue:
+ cost, current = heapq.heappop(connection_queue)
+ if current in seen:
+ continue
+
+ res += cost
+ seen.add(current)
+
+ for connection in adjacency_list[current]:
+ if connection[1] not in seen:
heapq.heappush(connection_queue, connection)
-
- while len(seen) < n and connection_queue:
- cost, current = heapq.heappop(connection_queue)
- if current in seen:
- continue
-
- res += cost
- seen.add(current)
-
- for connection in adjacency_list[current]:
- if connection[1] not in seen:
- heapq.heappush(connection_queue, connection)
-
- if len(seen) < n: return -1
- return res
+
+ if len(seen) < n: return -1
+ return res
def minimumCost(self, n: int, connections: List[List[int]]) -> int:
- adjacency_list = {}
-
- for connection in connections:
- if connection[0] not in adjacency_list:
- adjacency_list[connection[0]] = []
- if connection[1] not in adjacency_list:
- adjacency_list[connection[1]] = []
- adjacency_list[connection[0]].append((connection[2], connection[1]))
- adjacency_list[connection[1]].append((connection[2], connection[0]))
+ adjacency_list = {}
+
+ for connection in connections:
+ if connection[0] not in adjacency_list:
+ adjacency_list[connection[0]] = []
+ if connection[1] not in adjacency_list:
+ adjacency_list[connection[1]] = []
+ adjacency_list[connection[0]].append((connection[2], connection[1]))
+ adjacency_list[connection[1]].append((connection[2], connection[0]))
- return self.connecting_cities_with_minimum_cost(adjacency_list)
+ return self.connecting_cities_with_minimum_cost(adjacency_list)
```
## Example 2: [1584 - Min Cost to Connect All Points](https://leetcode.com/problems/min-cost-to-connect-all-points)
### Instructions
-You are given an array $points$ representing integer coordinates of some points on a 2D-plane, where $points[i]$ = $[xi, yi]$.
-The cost of connecting two points $[xi, yi]$ and $[xj, yj]$ is the **Manhattan distance** between them: $|xi - xj|$ + $|yi - yj|$, where $|val|$ denotes the absolute value of $val$.
+You are given an array $points$ representing integer coordinates of some points on a 2D-plane, where $points[i]$ = $[x_i, y_i]$.
+The cost of connecting two points $[x_i, y_i]$ and $[x_j, y_j]$ is the **Manhattan distance** between them: $|x_i - x_j|$ + $|y_i - y_j|$, where $|val|$ denotes the absolute value of $val$.
Return the minimum cost to make all points connected. All points are connected if there is exactly one simple path between any two points.
@@ -225,18 +226,19 @@ Return the minimum cost to make all points connected. All points are connected i
points = [[0,0],[2,2],[3,10],[5,2],[7,0]]
adjacency_list = {}
-for i in range(len(points)):
- current = tuple(points[i])
- for j in range(i+1, len(points)):
- destination = tuple(points[j])
- if current not in adjacency_list:
- adjacency_list[current] = []
- if destination not in adjacency_list:
- adjacency_list[destination] = []
-
- # The formula in the second item of the append, is to calculate the Manhattan Distance between two points (the edge weight)
- adjacency_list[current].append([abs(destination[0] - current[0]) + abs(destination[1] - current[1]), destination])
- adjacency_list[destination].append([abs(destination[0] - current[0]) + abs(destination[1] - current[1]), current])
+n = len(points)
+for i in range(n):
+ current = tuple(points[i])
+ for j in range(i + 1, n):
+ destination = tuple(points[j])
+ if current not in adjacency_list:
+ adjacency_list[current] = []
+ if destination not in adjacency_list:
+ adjacency_list[destination] = []
+
+ # The formula in the second item of the append, is to calculate the Manhattan Distance between two points (the edge weight)
+ adjacency_list[current].append([abs(destination[0] - current[0]) + abs(destination[1] - current[1]), destination])
+ adjacency_list[destination].append([abs(destination[0] - current[0]) + abs(destination[1] - current[1]), current])
```
@@ -259,21 +261,21 @@ The rest of the code follows an almost identical pattern as the previous one. Th
```py
# Here, our helper function contains one additional argument - the initial point (as here we don't need to randomly start)
def min_cost_points(adjacency_list, initial):
- # Number of nodes in the given tree
- n = len(adjacency_list)
- # A list we will use to implement a priority queue
- connection_queue = []
- # Total minimum cost to connect all points
- res = 0
- start = tuple(initial)
- # To ensure we don't create closed loops
- seen = set([start])
+ # Number of nodes in the given tree
+ n = len(adjacency_list)
+ # A list we will use to implement a priority queue
+ connection_queue = []
+ # Total minimum cost to connect all points
+ res = 0
+ start = tuple(initial)
+ # To ensure we don't create closed loops
+ seen = set([start])
```
-The below is the implementation of the main function. It is identical to the previous example in every way except for the final output (as in this question, we are guaranteed a solution)
+Below, is the implementation of the main function. It is identical to the previous example in every way except for the final output (as in this question, we are guaranteed a solution)
@@ -281,19 +283,19 @@ The below is the implementation of the main function. It is identical to the pre
```py
for connection in adjacency_list[start]:
- heapq.heappush(connection_queue, connection)
+ heapq.heappush(connection_queue, connection)
while len(seen) < n and connection_queue:
- cost, current = heapq.heappop(connection_queue)
- if current in seen:
- continue
+ cost, current = heapq.heappop(connection_queue)
+ if current in seen:
+ continue
- res += cost
- seen.add(current)
+ res += cost
+ seen.add(current)
- for connection in adjacency_list[current]:
- if connection[1] not in seen:
- heapq.heappush(connection_queue, connection)
+ for connection in adjacency_list[current]:
+ if connection[1] not in seen:
+ heapq.heappush(connection_queue, connection)
return res
```
@@ -310,52 +312,54 @@ The below is the implementation of the main function. It is identical to the pre
import heapq
class Solution:
- def min_cost_points(self, adjacency_list, initial):
- # Number of nodes in the given tree
- n = len(adjacency_list)
- # A list we will use to implement a priority queue
- connection_queue = []
- # Total minimum cost to connect all points
- res = 0
- # Taking the assumption that the n nodes in the adjacency list are from 1 to n
- start = tuple(initial)
- # To ensure we don't create closed loops
- seen = set([start])
-
- for connection in adjacency_list[start]:
- heapq.heappush(connection_queue, connection)
-
- while len(seen) < n and connection_queue:
- cost, current = heapq.heappop(connection_queue)
- if current in seen:
- continue
-
- res += cost
- seen.add(current)
-
- for connection in adjacency_list[current]:
- if connection[1] not in seen:
- heapq.heappush(connection_queue, connection)
-
- return res
-
- def minCostConnectPoints(self, points: List[List[int]]) -> int:
- adjacency_list = {}
- for i in range(len(points)):
- current = tuple(points[i])
- for j in range(i+1, len(points)):
- destination = tuple(points[j])
- if current not in adjacency_list:
- adjacency_list[current] = []
- if destination not in adjacency_list:
- adjacency_list[destination] = []
-
- adjacency_list[current].append([abs(destination[0] - current[0]) + abs(destination[1] - current[1]), destination])
- adjacency_list[destination].append([abs(destination[0] - current[0]) + abs(destination[1] - current[1]), current])
-
- if len(points) < 2:
- return 0
- return self.min_cost_points(adjacency_list, points[0])
+ def min_cost_points(self, adjacency_list, initial):
+ # Number of nodes in the given tree
+ n = len(adjacency_list)
+ # A list we will use to implement a priority queue
+ connection_queue = []
+ # Total minimum cost to connect all points
+ res = 0
+ # Taking the assumption that the n nodes in the adjacency list are from 1 to n
+ start = tuple(initial)
+ # To ensure we don't create closed loops
+ seen = set([start])
+
+ for connection in adjacency_list[start]:
+ heapq.heappush(connection_queue, connection)
+
+ while len(seen) < n and connection_queue:
+ cost, current = heapq.heappop(connection_queue)
+ if current in seen:
+ continue
+
+ res += cost
+ seen.add(current)
+
+ for connection in adjacency_list[current]:
+ if connection[1] not in seen:
+ heapq.heappush(connection_queue, connection)
+
+ return res
+
+ def minCostConnectPoints(self, points: List[List[int]]) -> int:
+ # Inititalizing an empty adjacency list to transform the points into something more convenient to work with
+ adjacency_list = {}
+ # Total number of items in the list of points (each coordinate pair is a point)
+ n = len(points)
+ for i in range(n):
+ current = tuple(points[i])
+ for j in range(i + 1, n):
+ destination = tuple(points[j])
+ if current not in adjacency_list:
+ adjacency_list[current] = []
+ if destination not in adjacency_list:
+ adjacency_list[destination] = []
+
+ adjacency_list[current].append([abs(destination[0] - current[0]) + abs(destination[1] - current[1]), destination])
+ adjacency_list[destination].append([abs(destination[0] - current[0]) + abs(destination[1] - current[1]), current])
+
+ if n < 2: return 0
+ return self.min_cost_points(adjacency_list, points[0])
```